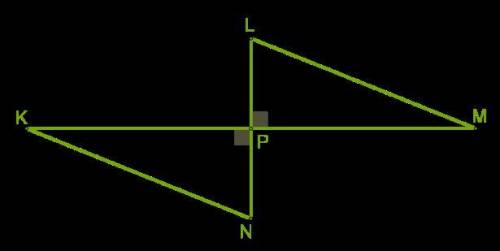
Два перпендикулярных отрезка KM и LN пересекаются в общей серединной точке P.
Какой величины∡ N и ∡ K, если ∡ L = 20° и ∡ M = 70°?

1. Отрезки делятся пополам, значит, KP = , = LP,
∡ = ∡ MLP, так как прямые перпендикулярны и каждый из этих углов равен °.
По первому признаку равенства треугольник KPN равен треугольнику MPL.

2. В равных треугольниках соответствующие углы равны.
В этих треугольниках соответствующие ∡ и ∡ M, ∡ и∡ L.
∡ K = °;
∡ N = °.

davidmarabyan    3   14.12.2020 03:32    22