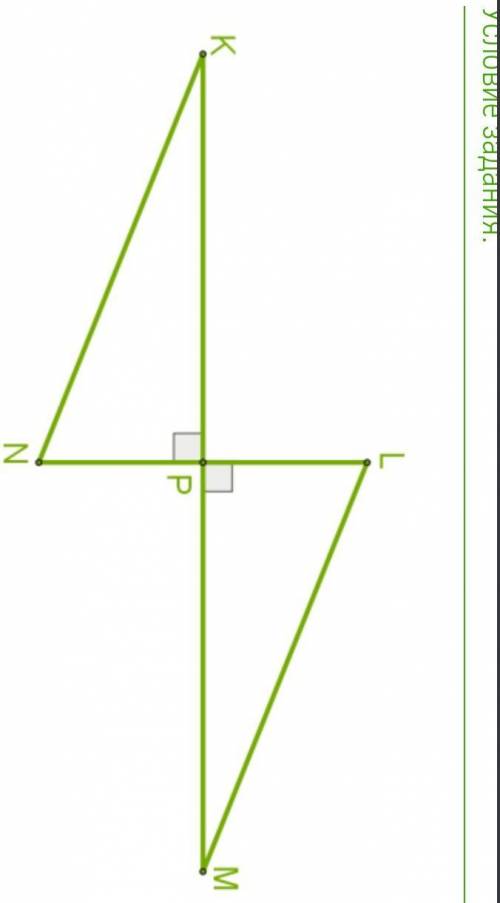
Два перпендикулярных отрезка KM и LN пересекаются в общей серединной точке P и образуют два равных треугольника KPN и MPL. Расстояние между точками K и L равно 34,3 см. Какое расстояние между точками M и N?

1. У равных треугольников все соответствующие элементы равны, стороны KP =
и NP =
как соответствующие стороны равных треугольников.

∡К
=
° и ∡
=
°, так как смежные с ними углы ∡ KPN = ∡ MPL =
°.

По первому признаку треугольник KPL равен треугольнику
.

2. В равных треугольниках соответствующие стороны равны. Для стороны KL соответствующая сторона — MN.
MN =
см.​

FlUSHWER    2   19.11.2020 17:50    6