Два квадрата имеют общую вершину. На прямую АС, проходящую через две другие их
вершины, опустили перпендикуляры ЕК и DН.
Докажите, что АH = СK
Другие вопросы по теме Геометрия
Популярные вопросы
- Синтаксический разбор предложения новость оглушила его как обухом по темени 20...
3 - 1.записать в виде степени с основанием 3 а) 3в 5 степени3в17степени 3(все это...
2 - Қазақстанның қазіргі сәулет өнері эссе (8-9 предложений) (8-9сөйлем)...
1 - Вактовом зале школы первые 5 рядов составлены из кресел красного цвета остальные...
1 - Найди периметр и площадь прямоугольника со сторонами a и b если а=16 дм и b =...
1 - Попс формуласын қолданып, оралдан қандай екенін айт. өз пікіріңді дәлелде. бірінші...
1 - 1. составьте две цепи питания из предложенного перечня организмов: белка, лягушка,...
1 - Почему хаммурапи за одно и тоже преступление предусматривал разные наказания...
3 - Всреднем из 600 батареек аа поступивших в продажу 30 неисправны найдите вероятностьтого...
1 - Подобрать стихотворение,которое ,на ваш взгляд, подходит для создания романса....
2
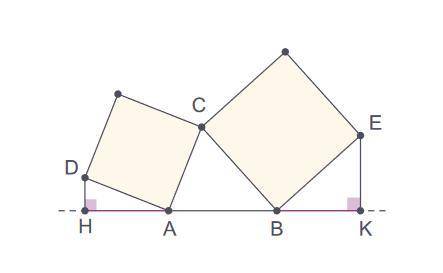
Два квадрата имеют общую вершину C. На прямую АB, проходящую через две другие их вершины, опустили перпендикуляры DH и EK. Докажите, что АH=BK.
Опустим перпендикуляр СL на AB.
∠CAD=90° (угол квадрата)
∠DAH +∠CAL =180° -∠CAD =90°
∠DAH +∠ADH =90° (острые углы △ADH)
∠ADH=∠CAL
AD=AC (стороны квадрата)
△ADH=△CAL (по гипотенузе и острому углу) => AH=CL
Аналогично △BEK=△CBL => BK=CL
Следовательно AH=BK