Два кола, радіуси яких дорівнюють R і r(r < R), дотикаються зовні. Знайдіть радіус більшого з кіл, що дотикаються до цих кіл та їхньої спільної зовнішньої дотичної.
Другие вопросы по теме Геометрия
Популярные вопросы
- Якими були наслідки монгольської навали на Галицько Волонську державу...
3 - Решите уравнение (2+с)^3-c^=6с^2...
3 - Ұшқан ұядағы 1 жағымсыз 1 жағымды және 1 даулы оқиға...
1 - Розвяжіть систему рівнянь у=х^2 2х+у=0...
2 - Что изображено на рисунке? Определи расход энергии по рисунку если что на счетчике...
3 - (NЕсепте.5%15%144500 кг29 000 тг360 000 м...
1 - Разложи на множители многочлен 28х^2+28хy+7y^2 ...
3 - КАК РЕШИТЬ УРОВНЕНИЯ 18*4+У=100...
2 - Put the verbs past simple...
3 - Какого назначение деловой графики...
3
Позначимо шуканий радіус як t.
З'єднавши центри кіл, та провівши від них перпендикуляри до дотичної, отримаємо прямокутну трапецію, основи якої дорівнюють R та r, а похила бічна - R + r.
Бічна що залишилась, знаходиться з до теореми Піфагора: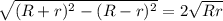
Всередині основної трапеції, є дві менших, з основами R і t, та r і t. Їх похилі, відповідно рівні R + t та r + t.
Тепер використовуючи все ту ж теорему Піфагора, зіставляємо рівняння:
Ось і наш радіус.