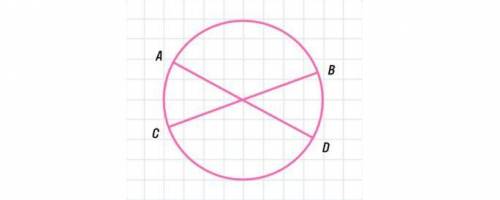
Два диаметра окружности AD и СВ пересекаются под углом 70°. Найди ∠ADB/
Другие вопросы по теме Геометрия
Популярные вопросы
- Тест 11 8 класс ким по . соединения элементов...
1 - Умоляю ! дайте развернутый ответ площадь сказочного города твист 41,6×10¹³см²...
3 - Написать сказку с храбрым героем! ! ...
3 - Подобрать отрывок из художественного произведения. переписать его и подчеркнуть...
3 - Укаком слове больше звуков чем букв горобина .. лищину..дубочки...
2 - Без списывания. в равнобедренном треугольнике abc (ab=bc) проведены биссектрисы...
2 - Решите любые 2 с плюсиком нас загрызёт...
3 - Выражение: (-5+0,2а²)(25+0,04а⁴+а²)...
2 - Какого стиля, жанра и тип текста “бәтеңке, шұжық, қаймақ” (ответ на казахском)...
2 - Аргумент к сочинению-рассуждению в доме чехова напишите ....
1
89
Объяснение:
Дано: Две диаметра окружности AD и СВ пересекаются под углом 70°.
Нам нужно найти угол ∠ADB.
Для начала, давайте определим, что такое диаметр. Диаметр - это отрезок, соединяющий две точки на окружности и проходящий через ее центр.
В нашей задаче у нас есть два диаметра, AD и СВ. Они пересекаются под углом 70°.
Для решения этой задачи мы можем использовать знания о геометрических свойствах окружностей и треугольников.
1. Посмотрите на треугольник ADB. Мы знаем, что отрезок AB - это диаметр окружности, поэтому он равен двум радиусам. Пусть радиус окружности равен r.
AB = 2r
2. Мы также знаем, что два диаметра AD и СВ пересекаются под углом 70°.
Мы можем использовать геометрическое свойство, согласно которому угол, образованный диаметром, равен 90°. Значит, мера угла ADC равна 90°.
3. Из угла ADC мы можем найти угол ADB, используя свойства параллельных прямых.
Поскольку AB - это диаметр окружности, угол BAC (или CAD) также равен 90°.
Это означает, что угол ADB является внутренним углом треугольника ABD и поэтому его мера равна 180° - (мера угла DAB + мера угла BAD).
4. Теперь давайте воспользуемся свойством треугольников, согласно которому сумма мер внутренних углов треугольника равна 180°.
Это означает, что мера угла DAB + мера угла BAD + мера угла ABD равна 180°.
Применив это свойство, мы можем записать уравнение:
70° + 90° + мера угла ABD = 180°
5. Теперь мы можем решить это уравнение, чтобы найти меру угла ABD.
70° + 90° + мера угла ABD = 180°
160° + мера угла ABD = 180°
мера угла ABD = 20°
Таким образом, угол ∠ADB равен 20°.