Дві сторони трикутника дорівнюють 3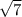 і 12 см, а бісектриси при третій стороні перетинаються під кутом 30 градусів.Знайдіть площу трикутника.
і 12 см, а бісектриси при третій стороні перетинаються під кутом 30 градусів.Знайдіть площу трикутника.
Другие вопросы по теме Геометрия
Популярные вопросы
- 1:В треугольнике ABC средняя линия KM, параллельная AB, на 27 меньше AB. Найти...
2 - это контрольнаярассказ надо перевести на русский...
2 - 8. Даны растворы серной кислоты и азотной кислоты. При добавлении к этим кислотам...
2 - 1- mashq. Tushum kelishigi ishtirokida 4-5 ta gap tuzing. Namuna: Men bu kitobni...
3 - Уақыты тиімді пайдалану деген не?...
3 - Стрелок один раз стреляет в круглую мишень. При этом вероятности попадания в зоны...
2 - Установите соответствие: нефть, Базальт, уголь, мел, Базальт. 1)осадочные 2)магматические...
3 - 2 эпитита и 2 сравнения в стихе мороз красный нос...
1 - b) Write true answers to the questions from Example: a) I was born in Bishkek...
2 - Найди длину отрезка,если пятая часть его 5см...
1
ответ: 9√21 (см²)
Объяснение (подробно): Нарисуем треугольник АВС. Пусть АВ=3√7, ВС=12, О- точка пересечения биссектрис из А и С.
Рассмотрим треугольник АОС. Угол ЕОС - внешний. По свойству внешнего угла сумма двух внутренних углов, не смежных с ним, равна 30°. Эти углы - половины углов при стороне АС треугольника АВС .Поэтому угол ВАС+ВСА=60°. Из суммы углов треугольника угол АВС=180°-60°=120°.
Одна из формул площади треугольника S=0,5•a•b•sinα, где а и b - стороны, α – угол между ними. S (ABC)=0,5•3√7•12•√3/2=9√21 (см²)
=========
Задача решена по данному в вопросе условию. Возможно, условие дано с ошибкой и одна из сторон не 3√7, а 7√3. Тогда площадь будет иной. Вычислите ее самостоятельно.