.
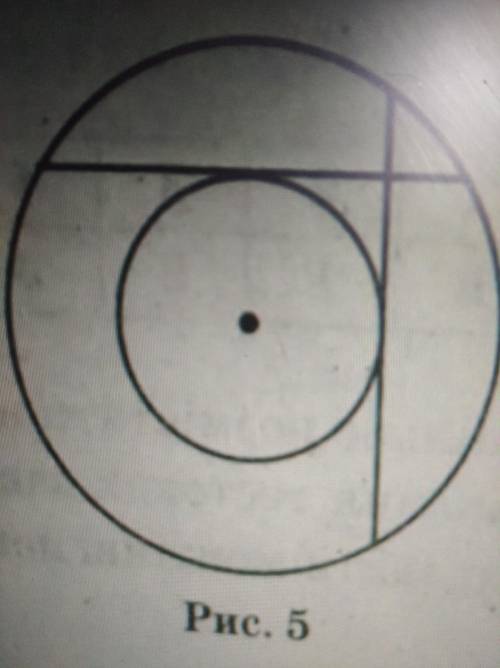
Дві рівні та взаємно перпендикулярні хорди кола точкою перетину діляться на частини завдовжки 4см і 16 см . Знайдіть рідіус кола , яке дотикається до цих хорд і має спільний центр із поданим колом .
Другие вопросы по теме Геометрия
Популярные вопросы
- Всемье 3 детей для. новогоднего подарка приготовили 12 мандаринов...
2 - Какое течение у оки быстрое или медленное...
3 - Доклад на тему экологические проблемы зоны степей...
1 - Сколько будет? 1целая семь восьмых минус 3целых одна третья! ?...
1 - Составьте программу вычисления количества трехзначных чисел, у...
2 - По - сочинение на тему: цивилизация индии и китая...
1 - Придумать слова с приставкой,корнем,с одним суфиксом который в...
1 - Составить 5-6 предложений в котором рассказывается пример почему...
1 - Какие три события относятся к правлению петра 1. 1) манифест о...
2 - Надо! составьте 4 предложения со словом комбинация! ! надо!...
2
6 см
Объяснение:
Радиусы OK и ОМ, проведённые в точки касания хорд с малой окружностью, будут перпендикулярны касательным - хордам АВ и CD. Но также, по свойству диаметра, перпендикулярного хорде, точки К и М будут лежать на серединах отрезков АВ и CD.
АВ=CD=AL+LB=16+4=20см
AK=KB=20/2=10см
KL=KB-LB=10-4=6см
KLMO - квадрат, поскольку все его смежные стороны имеют между собой прямой угол (2 - как радиусы к касательным, 1 - по условию перпендикулярности хорд, и оставшийся тоже получается 90°), и две его смежные стороны ОК и ОМ равны радиусу.
Значит ОМ=KL=6см