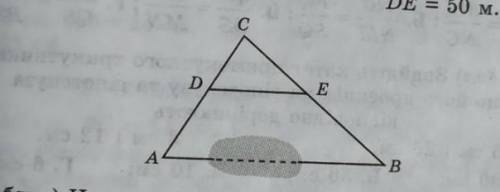
ДУЖЕ ПОТРІБНО. Визначте відстань від точки А до недоступної точки В (рис. 5), якщо СА = 60 м, СВ = 90 м, CD = 20 м, СЕ = 30 м, DE = 40 м. Про¬ведіть необхідні доведення.​

Добрый день, ученик!

Для определения расстояния от точки А до недоступной точки В, нам понадобится использовать теорему косинусов. Позволь мне объяснить данную теорему и применить ее для решения данной задачи.

Теорема косинусов гласит: внутренний угол треугольника равен сумме квадратов длин двух его сторон, умноженных на косинус этого угла, минус удвоенное произведение длин этих двух сторон на косинус дополнительного угла.

В данной задаче, треугольник СДЕ - прямоугольный треугольник, так как угол E равен 90 градусов (прямой угол). Также рассмотрим треугольник САВ.

Для решения задачи, нам понадобится найти длину стороны ВС. Мы можем найти эту сторону, применяя теорему Пифагора для треугольника СДЕ:

DE² + CD² = CE²
40² + 20² = CE²
1600 + 400 = CE²
2000 = CE²
CE = √2000

Теперь мы можем решить треугольник САВ, используя теорему косинусов:

AB² = AC² + BC² - 2 × AC × BC × cos(∠ВАС)

Мы знаем, что AC = 60 м, BC = √2000 м (по результату вычисления стороны ВС) и ∠ВАС = 90 градусов.

Теперь подставим значения в формулу:

AB² = 60² + (√2000)² - 2 × 60 × √2000 × cos(90°)
AB² = 3600 + 2000 - 120 × √2000 × 0
AB² = 5600

Для того чтобы найти AB, возьмем квадратный корень из обеих сторон:

AB = √5600
AB = 2 × √1400
AB = 2 × √4 × √350
AB = 2 × 2 × √350
AB = 4√350

Таким образом, расстояние от точки А до недоступной точки В равно 4√350 м.

Надеюсь, что данное пошаговое решение помогло тебе понять, как решить данную задачу. Если у тебя есть еще вопросы, не стесняйся задавать их. Удачи в учебе!