1. Геометрия
  2. Довжина діагоналі квадрата

Довжина діагоналі квадрата дорівнює
сантимерів. Обчисліть його площу


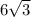
6 \sqrt{3}

RaminaMirzaeva RaminaMirzaeva    1   07.04.2022 10:11    0

Ответы
svashalol svashalol  07.04.2022 10:20

54 см^2

Объяснение:

У квадрата стороны равны.

По теореме Пифагора есть уравнение:

{a}^{2} + {a}^{2} = (6 \sqrt{3} ) {}^{2} \\ 2a {}^{2} = 6 {}^{2} { (\sqrt{3}) }^{2} \\ 2a {}^{2} = 36 \times 3 \\ 2a {}^{2} = 108 \\ {a}^{2} = 108 \div 2 \\ {a}^{2} = 54 \\ a = \sqrt{54}

Поскольку длина стороны не может быть отрицательной, то -√54 не удовлетворяет условию.

Площадь квадрата равна S = a^2, отсюда

( \sqrt{54} ) {}^{2} = 54.


Довжина діагоналі квадрата дорівнює сантимерів. Обчисліть його площу
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
elena407 elena407  20.06.2019 05:10
Гипотенуза прямоугольного треугольника равна 6. два угла этого треугольника равны 45 гр. найти катеты этого треугольника....
vovkahooligan vovkahooligan  20.06.2019 05:10
Сдо вершин треугольника и до прямой мр , если мк = 20 см , мр=12см, кс=16см....
dmitriidimaro dmitriidimaro  09.11.2020 19:52
1. Діагональ прямокутного паралелепіпеда d і утворює з бічними гранями кути a i b. А. Одна з сторін основи дорівнює d ѕіn а.Б. Діагональ основи паралелепіпеда дорівнює...
musulmanka95 musulmanka95  09.11.2020 19:46
ГЕОМЕТРИЯ ГЕОМЕТРИЯ 10 КЛАСС ГЕОМЕТРИЯ УМОЛЯЮ ГЕОМЕТРИЯ 10 КЛАСС...
Vanek041005 Vanek041005  09.11.2020 19:43
#1) Один із суміжних кутів у 5 разів більший від іншого. Знайти ці кути #2) Знайти суміжні кути, якщо їх градусні міри відносяться як 3:6. нужно...
ddiana004 ddiana004  09.11.2020 19:42
ів якщо правильно розв‘яжете....
лох2008 лох2008  09.11.2020 19:42
Дано точки O(0;0), A(a1;a2), B(b1;b2). Виразіть через їх координати суми: а) OA+AB, б) OB+BA, в) AB+BO...
Мамиами Мамиами  02.10.2019 09:40
Діагональ трапеції вписаної в коло перпендикулярна до бічної сторони. де лежить центр кола?...
Danila5555 Danila5555  21.08.2019 22:20
Периметры подобных треугольников равны 12см и 24см. сторона большего треугольника равна 8 см. чему равна сходственная ей сторона...
Анна12011 Анна12011  21.08.2019 22:20
Найти основание трапеции если средняя линия 11см, а одна из оснований 7 см....

Популярные вопросы