Доведіть, що для будь-яких n точок А1, А2, ..., A, існуе єдина точка М така, що (вектори) МА 1+ МА2 +...+ MAn=0 ( точку М зивають центроїдом системи точок А1, А2, ...,An).
Другие вопросы по теме Геометрия
Популярные вопросы
- Напишите сочинение мой друг по этому плану: 1.как мы познакомились 2 внешность,черты...
2 - Почему португальский король не заинтерисовался предложением х. колумба о...
1 - 120 ц воды полностью заполняют 10 одинаковых цистерн.сколько центеровс воды...
3 - Длина прямоугольника 3м а его ширина состовляет 2/5 его длины какова площядь...
1 - Как сделать слово көзілдірік и сомке по тауельдик жалгау...
2 - Определи склонение у словах стулья лестницы сметаны веревки доктора и учителя...
2 - Переведите на қазақ тілінің мемлекет деңгейіндегі беделі өте жоғары дәрежеде...
2 - Скакой минимальной силой надо тянуть по люду стоящего на коньках ученика...
2 - Из какого числа надо вычесть 35 чтобы получить 22?...
1 - Найти значение выражение 1-5x2 при x=-4...
1
Существование: пусть даны точки с координатами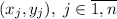 , а координата точки
, а координата точки 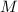 есть
есть 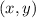 . Тогда получаем систему линейных уравнений:
. Тогда получаем систему линейных уравнений: ![\begin{cases}\sum\limits_{j=1}^{n}[x_{j}-x]=0\\ \sum\limits_{j=1}^{n}[y_{j}-y]=0\end{cases}](/tpl/images/4754/9347/1af90.png) , откуда
, откуда 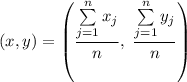 .
.
Единственность: пусть нашлась вторая такая точка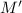 . Тогда
. Тогда 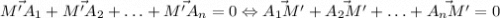 . Сумма последнего равенства с исходным в условии дает
. Сумма последнего равенства с исходным в условии дает 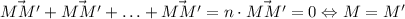 .
.