дорешать! ТЕМА: ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ.

Нужно заполнить пропуски самостоятельно. (_)
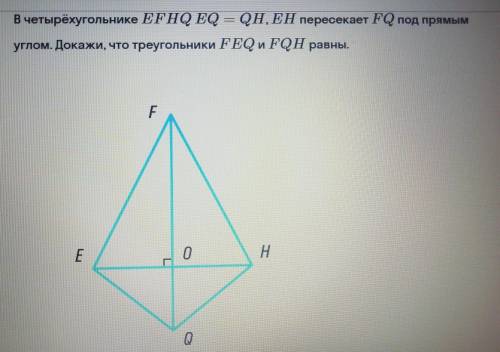
Дано:
EFHQ=

EQ=QH

EH FQ

Доказать: FEQ=FQH

ДОКАЗАТЕЛЬСТВО:

1. Так как EQ=QH, то EQH-(по определению).

Значит, QO- высота и биссектриса (по свойству равнобедренного треугольника),
Следовательно, <EQO=_ [Я вставила: углу<HOQ] (по свойству).

2.FEQ=FHQ (по 2м сторонам и углу между ними), так как:

А) _=QH (по условию) [я вставила EQ]

Б) <= <HQO (по доказанному) [Я вставила <EQO]

В) ___-общая. [ Я вставила FQ]

дорешать! ТЕМА: ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ. Нужно заполнить пропуски самостоятельно. (___) Дан

Ответы

leramakarova2001 02.01.2024 18:56

Доказательство:

1. Так как EQ=QH, то EQH- (по определению). Значит, QO - высота и биссектриса (по свойству равнобедренного треугольника), следовательно,
2. FEQ=FHQ (по 2м сторонам и углу между ними), так как:
А) EQ=QH (по условию).
Б) В) FQ - общая сторона.

Таким образом, мы доказали, что FEQ=FHQ, что и требовалось доказать.

Теперь разберем каждый шаг доказательства подробнее:

1. Мы знаем, что EQ=QH (по условию). Также мы знаем, что QO - высота и биссектриса. В равнобедренном треугольнике, биссектриса также является высотой и делит основание на две равные части. Поэтому
2. В этом шаге мы доказываем, что FEQ=FHQ, используя две стороны и угол между ними.
А) Мы знаем, что EQ=QH (по условию).
Б) Мы доказали ранее, что В) FQ - общая сторона у обоих треугольников.

Итак, мы доказали, что FEQ=FHQ.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия