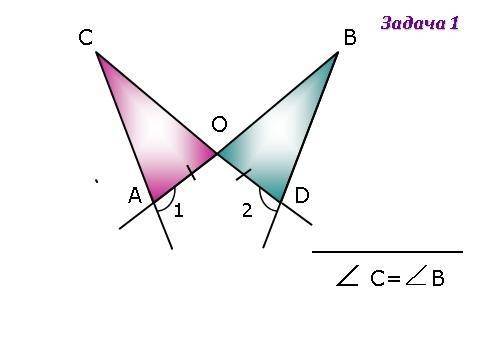
докозать что угол C = углу В

Для того чтобы доказать, что угол C равен углу В, мы можем использовать свойство треугольников, а именно равенство углов треугольников. В данном случае, у нас есть два треугольника, ABC и BCD.

Шаг 1: Рассмотрим треугольник ABC. У нас есть две известные величины углов: угол А и угол В.

Шаг 2: Используем свойство, которое гласит, что сумма углов треугольника равна 180 градусам. Запишем это свойство в виде уравнения: А + В + C = 180.

Шаг 3: Теперь рассмотрим треугольник BCD. У нас есть три угла: угол В, угол С и угол D.

Шаг 4: Используем свойство, которое гласит, что сумма углов треугольника равна 180 градусам. Запишем это свойство в виде уравнения: В + С + D = 180.

Шаг 5: Теперь у нас есть два уравнения: А + В + C = 180 и В + С + D = 180.

Шаг 6: Мы хотим доказать, что угол C равен углу В, то есть C = В. Для этого нам нужно найти какую-то связь между углами А, В, С и D.

Шаг 7: Обратимся к треугольнику ABC. Из уравнения А + В + C = 180 мы можем выразить угол C: C = 180 - А - В.

Шаг 8: Подставляем значение C в уравнение В + С + D = 180: В + (180 - А - В) + D = 180.

Шаг 9: Упрощаем уравнение: 180 - А + D = 180.

Шаг 10: Вычитаем 180 с обеих сторон уравнения: -А + D = 0.

Шаг 11: Переносим -А на другую сторону уравнения: D = А.

Шаг 12: Мы получили, что угол D равен углу А, то есть D = А.

Шаг 13: Так как D = А и В = А, то получается, что D = В.

Шаг 14: Из уравнения D = В следует, что С = В.

Шаг 15: Таким образом, мы доказали, что угол C равен углу В.