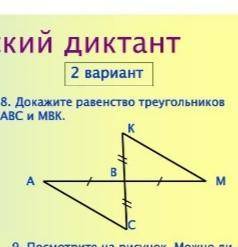
Докажите равенство треугольников ABC И MBK

Угол ABC = KBM как вертикальные следовательно по первому признаку равенства треугольников, треугольник ABC = KBM(AB = BM,BK = BC по условию; угол ABC = KBM как вертикальные)

Для доказательства равенства треугольников ABC и MBK, мы можем использовать одну из трех основных теорем подобия треугольников: теорема угла-угла (УУ), теорема сторона-угол-сторона (СУС), или теорема сторона-сторона-сторона (ССС). Давайте воспользуемся теоремой ССС для доказательства равенства треугольников ABC и MBK.

Шаг 1: Построение
На рисунке мы видим два треугольника ABC и MBK. Для удобства обозначим точку пересечения прямых AM и CK как точку D.

Шаг 2: Установление равенств
Для доказательства равенства треугольников, нам нужно установить, что соответствующие стороны и углы треугольников равны между собой.

а) Стороны:

AC = KC, так как они являются лучами прямых.

AB = MB, так как они являются горизонтальными отрезками.

BC = BK, так как они являются вертикальными отрезками.

Теперь, мы установили равенство соответствующих сторон треугольников.

б) Углы:
Угол ABC и угол MBK - это прямые углы (90 градусов), поэтому они равны.

Угол BAC и угол MBK - это прямые углы (90 градусов), поэтому они равны.

Угол ACB и угол KMB - это общие вертикальные углы, поэтому они равны.

Теперь, мы также установили равенство соответствующих углов треугольников.

Шаг 3: Вывод
Мы установили, что треугольники ABC и MBK равны между собой, используя теорему ССС (равенство сторон-сторон-сторон) и доказав, что соответствующие стороны и углы треугольников равны.

Таким образом, треугольники ABC и MBK - это равные треугольники.