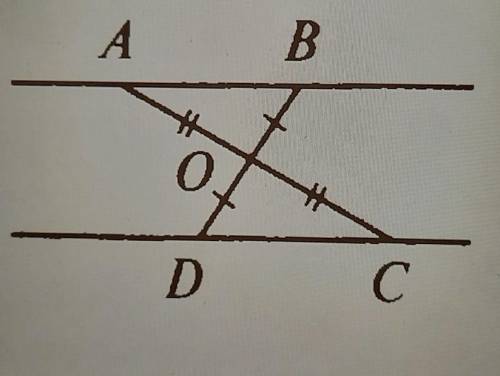
Докажите параллельность прямых AB и DC?

​

Чтобы доказать параллельность прямых AB и DC, мы можем использовать теорему о параллельных линиях. Согласно этой теореме, если углы, образованные пересекающимися прямыми и трансверсальной, равны между собой, то эти прямые параллельны.

На данной диаграмме у нас есть две пары вертикальных углов - угол A и угол C, а также угол B и угол D.

1. Предположим, что прямые AB и DC параллельны. В таком случае, вертикальные углы должны быть равными, поскольку они образуются параллельными прямыми и трансверсальной (горизонтальной) прямой.

2. Угол A и угол C имеют одинаковую меру. Это можно видеть из диаграммы, поскольку они оба являются вертикальными углами.

3. Угол B и угол D также имеют одинаковую меру. Это также следует из того факта, что они являются вертикальными углами.

4. Таким образом, все вертикальные углы равны между собой, что говорит о параллельности прямых AB и DC.

Заключение: Прямые AB и DC параллельны на основании равенства вертикальных углов, что подтверждает теорему о параллельных линиях.

Это детальное объяснение позволяет школьнику понять логическую последовательность решения и основано на понятиях углов и параллельных линиях.