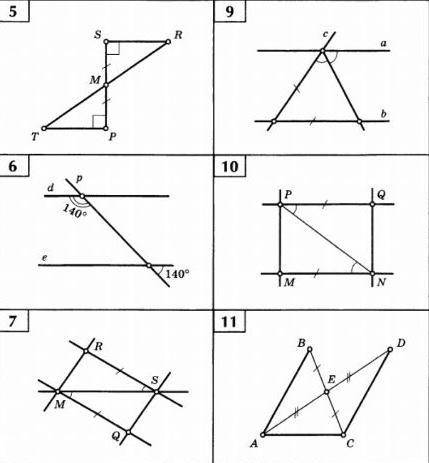
ДОКАЖИТЕ ПАРАЛЛЕЛЬНОСТЬ 6,7,9,10

Там везде углы смежные аос равно бод вот такие дела

Для доказательства параллельности линий 6, 7, 9 и 10 на рисунке, нам понадобятся некоторые геометрические теоремы и свойства.

Первым шагом, давайте рассмотрим значок угла между линиями 6 и 9. Допустим, что это угол A.

Теорема 1: Если углы между параллельными линиями и поперечной линией равны, то все поперечные линии параллельны.
Согласно этой теореме, чтобы показать, что линии 6 и 9 параллельны, мы должны показать, что углы А и В между ними равны.

Далее, мы замечаем, что угол В между линиями 6 и 7 является вертикальным углом для угла В между линиями 6 и 9 (поскольку они пересекаются).

Свойство 1: Вертикальные углы равны.
Следовательно, углы B между линиями 6 и 7 и углы B между линиями 6 и 9 равны.

Далее, на рисунке видно, что угол С между линиями 7 и 10 также является вертикальным углом для угла B между линиями 6 и 7.

Свойство 2: Вертикальные углы равны.
Следовательно, углы С между линиями 7 и 10 и углы B между линиями 6 и 7 равны.

Теперь мы можем сказать, что углы А, В и С между линиями 6, 7 и 9, 10 соответственно равны, так как они все являются вертикальными углами.

Свойство 3: Если две пары углов между линиями равны, то линии параллельны.
Таким образом, по свойству 3, мы можем заключить, что линии 6, 7, 9 и 10 параллельны, так как углы А, В и С, соответственно между линиями равны.

В итоге, мы доказали параллельность линий 6, 7, 9 и 10, используя свойства вертикальных углов и теорему о параллельных линиях и углах.

Обратите внимание, что в данном ответе предоставлено только одно возможное решение. В геометрии существует множество различных способов доказательства параллельности линий, и в определенных случаях необходимо использовать другие теоремы и свойства.