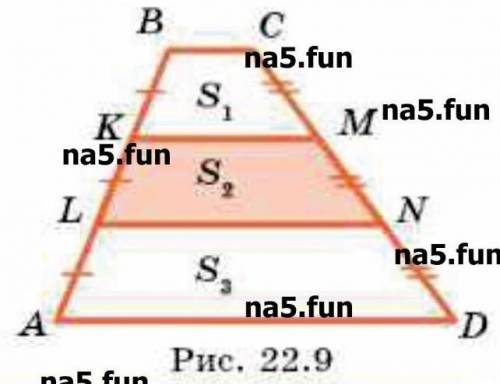
Докажите, что в трапеции АВСD
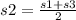
Другие вопросы по теме Геометрия
Популярные вопросы
- Напишите стилистически нейтральный синоним к слову грязища...
2 - Выражение: (4-n^6) (16+4n^6 +n^12) - 4(4-n^3)^2...
3 - Вчем действие соляной кислоты на карбонат натрия na2co3 сходно...
3 - Найдите ошибки и недочёты в употреблении сложных предложений....
2 - Скем сравнивает людей несмелых и несильных духом горький?...
3 - Читаючи роман жуля верна пятнадцатилетний капитан я...
1 - Выписать афоризмы из произведения маленький принц сент экзюпери...
1 - Придумать 6 предложений на языке на тему спорт )...
2 - Определите , какое число является лишним. а) 2,3, 6 , 7. 11 б)...
3 - Предложение с одиночным деепричастием ....
1
LN = a+b, то KM=a-b; AD=a+3b; BC=a-3b.
Высоты всех трех трапеций одинаковы; пусть они равны h. Тогда
что и требовалось доказать.
А еще проще можно рассуждать так. Проведем средние линии m, n и k верхней, средней и нижней трапеций. Очевидно, что средняя линия средней трапеции является также средней линией трапеции, чьими основаниями служат средние линии верхней и нижней трапеций. Остается вспомнить, что средняя линия трапеции равна полусумме оснований, а также то, что площадь трапеции равна произведению средней линии на высоту. Поэтому площадь верхней трапеции равна mh, площадь нижней трапеции равна kh, площадь средней трапеции равна