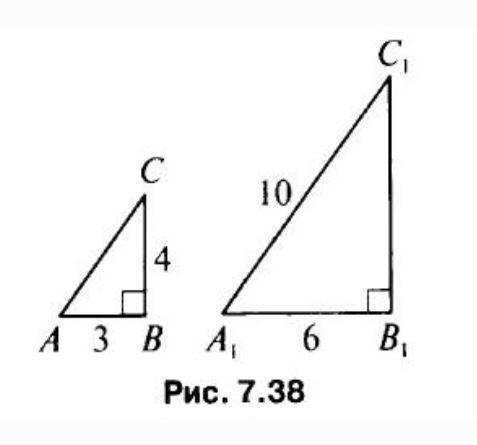
Докажите что треугольнике подобны, но не используя теорему Пифагора
Другие вопросы по теме Геометрия
Популярные вопросы
- Выполнить(написать) программу со своим символом.(В выводе должны...
1 - Задание № 1 - Выписать из текста 5 частиц и указать их разряд. Нужно...
3 - решить номер 4609,4616,4618...
3 - Как ты думаешь, , какую силу надо приложить к свободному концу троса,...
3 - 3) Укажите разряд выделенных местоимений и их синтаксическую роль...
1 - Сложи подобные слагаемые: −715y+13y. ответ (если в ответе получится...
1 - ТЕСТ! ПО ХИМИИ 11 КЛАСС! Работа тест для 11 класс по теме «Классификация...
3 - Теңдеудегі уайнымалысын xарқылы өрнектеп, теңдеудің кезкелген екі...
2 - Из картона вырежьте прямоугольник отрежьте 4 одинаковые нити проденьте...
1 - Закон кулона можно записать в виде F=k*(q1*q2/r^2)...
1
1. Угловое свойство: Угол А равен углу D, угол B равен углу E и угол C равен углу F. Это следует из того, что углы накрытых дуг на вписанных окружностях, проходящих через вершины треугольников, равны между собой.
2. Сторонное свойство: Пропорциональность сторон треугольников.
Мы можем разделить каждую сторону треугольника ABC на соответствующую сторону треугольника DEF и проверить, будут ли отношения всех трех сторон одинаковыми.
Рассмотрим отношение CD/AB:
CD = 4 см
AB = 8 см
CD/AB = 4/8 = 1/2
Теперь рассмотрим отношение EF/BC:
EF = 2 см
BC = 4 см
EF/BC = 2/4 = 1/2
И, наконец, рассмотрим отношение DE/AC:
DE = 3 см
AC = 6 см
DE/AC = 3/6 = 1/2
Мы видим, что все отношения сторон равны 1/2. Таким образом, стороны треугольника DEF пропорциональны соответствующим сторонам треугольника ABC.
Исходя из углового и сторонного свойств, мы можем сделать вывод, что треугольники ABC и DEF подобны.