Докажите что треугольник BCF равен треугольнику DCF
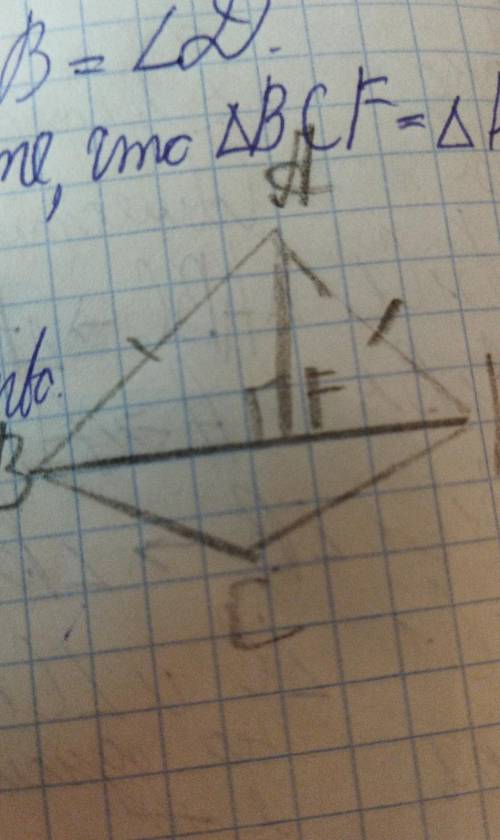
Другие вопросы по теме Геометрия
Популярные вопросы
- Быт татар, обычаи , какие особенности , характер( из рассказа ,,кавказский пленник...
2 - (россия нижний новгород), в какой природной зоне расположен твой регион?...
3 - Вслове сложа нужно проверить букву о...
1 - Какое из двух соединений —бензол или этилбензол—будет легче окисляться? напишите...
1 - Дайте характеристику птк своей местности согласно плану характеристики, используя...
1 - Выясните значениу слов реставрация, мушкет, мушкитёры....
2 - Ввыделенном предложении найдите слово, в котором не совпадает количество букв...
3 - Решить . длина катетов прямоугольного треугольника равны корень из 12 см и корень...
1 - Добавьте глагол в нужной форме l like- we look- they wash- you cry-he i hurry-...
2 - На завод отправлено 3600 тонн угля в вагонах по 6 тонн в каждом и столько же угля...
2
1. Стороны:
В треугольнике BCF, сторона BC отмечена синим цветом на рисунке. В треугольнике DCF, сторона DC отмечена красным цветом на рисунке. Задача доказать, что эти стороны равны.
Для этого, мы можем использовать информацию о том, что треугольник ABC равнобедренный и ABC = 90°. Зная, что угол ABC = угол ACB, мы можем заключить, что эти углы в треугольниках BCF и DCF тоже равны. Обозначим этот угол как θ.
Так как BC и DC являются биссектрисами угла ABC и ACB соответственно, мы можем заключить, что уголы BDC и BCF равны между собой. Обозначим этот угол как α.
Таким образом, у нас есть пара равных углов и пара равных сторон, что является достаточным условием равенства двух треугольников (по критерию ССС - сторона-сторона-сторона). Поэтому, сторона BC равна стороне DC (BC = DC).
2. Углы:
Мы уже установили, что угол BCF равен углу DCF (θ), так как они являются биссектрисами соответствующих углов в треугольниках ABC и ACD.
Выше мы обозначили равный угол между BDC и BCF как α.
Также, углы CBF и CDF равны друг другу, так как они оба равны половине угла ABC, который равен половине угла ACB (θ). Обозначим этот угол как β.
Таким образом, у нас есть две пары равных углов в треугольнике BCF и треугольнике DCF, что является вторым достаточным условием равенства двух треугольников (по критерию УГУ - угол-угол-угол). Поэтому, треугольник BCF равен треугольнику DCF.
Таким образом, мы доказали, что треугольник BCF равен треугольнику DCF, используя два критерия равенства треугольников - ССС и УГУ.