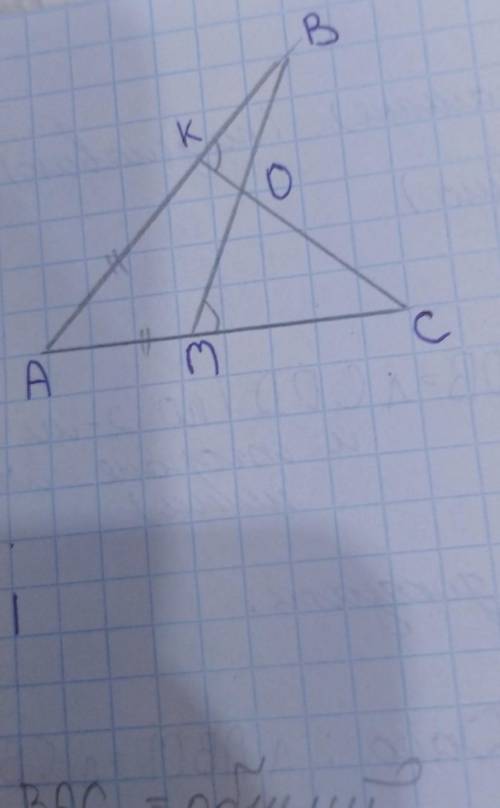
Докажите, что: Треугольник АВМ = треугольник АСК; треугольник КВО = треугольник МСО
Ответы
Для того чтобы доказать, что треугольник АВМ равен треугольнику АСК, мы должны проверить, что все их соответствующие стороны равны друг другу, и что все их соответствующие углы также равны.
1. Начнем сравнение сторон. Мы видим, что сторона АВ совпадает с АС, так как это общая сторона в треугольниках.
2. Теперь давайте рассмотрим стороны ВМ и СК. Они также совпадают, так как отрезок МК является биссектрисой угла ВМК, и биссектриса делит сторону ВК на две равные части. Таким образом, ВМ = МК = СК.
3. Также важно проверить, что углы треугольников АВМ и АСК равны. В треугольнике АВМ мы имеем углы ВАМ и МАВ, и в треугольнике АСК углы САК и КАС.
4. Обратимся к углу ВАМ в треугольнике АВМ. Он равен 50 градусам, так как это данное условие.
5. Теперь посмотрим на угол САК в треугольнике АСК. Угол САК равен 50 градусам. Почему? Потому что угол МАК является биссектрисой угла МАС, и биссектриса делит угол МАС пополам, что означает, что уголы САК и КАС равны.
Подводя итоги, мы доказали, что треугольник АВМ равен треугольнику АСК в соответствии с данным условием.
Теперь давайте рассмотрим доказательство равенства треугольников КВО и МСО.
1. Проверим, что стороны КВ и МС равны. Мы видим, что сторона МК совпадает с КВ, так как это общая сторона треугольников.
2. Теперь давайте рассмотрим стороны БО и ОС. Они также совпадают, так как отрезок МО является биссектрисой угла МБО, и биссектриса делит сторону БО на две равные части. Таким образом, БО = ОМ = ОС.
3. Также важно проверить, что углы треугольников КВО и МСО равны. В треугольнике КВО мы имеем углы БКВ и КВБ, а в треугольнике МСО углы БМС и МСБ.
4. Обратимся к углу БКВ в треугольнике КВО. Он равен 60 градусам, так как это данное условие.
5. Теперь рассмотрим угол БМС в треугольнике МСО. Угол БМС равен 60 градусам. Почему? Потому что угол БМС является биссектрисой угла БМО, и биссектриса делит угол БМО пополам, что означает, что углы БМС и МСБ равны.
Таким образом, мы доказали, что треугольник КВО равен треугольнику МСО в соответствии с данным условием.
Окончательно, мы доказали, что треугольник АВМ равен треугольнику АСК и треугольник КВО равен треугольнику МСО.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- Сочинение по теме: хорошие люди на страницах произведений лескова...
3 - Составь уравнение реши его и сделай проверку : из неизвестного...
3 - Максимум . найти средства художественно выразительности. (эпитет,...
2 - 6. прочитай. замени повторяющиеся имена существительные местоимениями...
1 - Кандай манызда уш жагдайда галамторды пайдаланасындар ауыспалы...
1 - Как оформить обложки книги федорина горе подскажите...
2 - До чого закликав князь ярослав мудрий своїх синів? чим це було...
1 - Ккакому из трех типов монархии относится владимиро суздальская...
2 - Замените выделенные глаголы глаголами...
3 - Осевое сечение цилиндра квадрат площадь которого 100 см в квадрате,...
3