Докажите что радиус окружности вписанной в ромб равен половине высоты ромба. и медиана прямоугольного треугольника проведенная к гипотенузе равна 7,1 см, а один из острых углов равен 36 градусов. используя микрокалькулятор найдите длины сторон и полощадь. ответ округлить до десятых. это

1) Поскольку окружность вписана в ромб, то его стороны являются касательными к окружности. Касательная перпендикулярна радиусу, проведённому в точку касания, значит диаметр вписанной окружности равен высоте ромба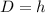 , а, соответственно радиус равен половине высоты ромба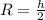 

2) В прямоугольном треугольнике медиана, падающая на гипотенузу, равна половине гипотенузы, значит гипотенуза равна 14,2 см

Дальше, я уж не знаю, можно ли вам при решении пользоваться таблицами Брадиса, но по-иному никак... В общем катеты соответственно равны:

сантиметров, разумеется.

Ну и, как "Лучшее решение" не забудь отметить, ОК?!.. ;)))