1. Геометрия
  2. Докажите, что четырехугольник

Докажите, что четырехугольник с вершинами е(-2 ; 0), f(2; 2), м(4; -2) и n(0; -4) является квадратом

Никита8547 Никита8547    3   18.05.2019 13:10    2

Ответы
Zaika14102001 Zaika14102001  11.06.2020 19:26

Вектор EF имеет координаты (2-(-2); 2-0) = (4; 2). Его длина
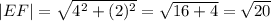
|EF|=\sqrt{4^2+(2)^2}=\sqrt{16+4}=\sqrt{20}\\
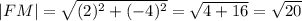
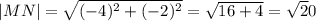
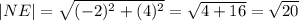
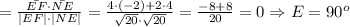
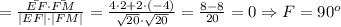
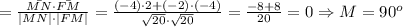
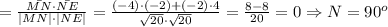
Вектор FM имеет координаты (4-2; -2-2) = (2; -4). Его длина
|FM|=\sqrt{(2)^2+(-4)^2}=\sqrt{4+16}=\sqrt{20}
Вектор MN имеет координаты (0-4; -4-(-2)) = (-4; -2). Его длина
|MN|=\sqrt{(-4)^2+(-2)^2}=\sqrt{16+4}=\sqrt20
Вектор NE имеет кооординаты (-2-0; 0-(-4)) = (-2; 4). Его длина
|NE|=\sqrt{(-2)^2+(4)^2}=\sqrt{4+16}=\sqrt{20}
Все стороны четырёхугольника равны. Найдём углы между ними:
\cosE=\frac{\bar{EF}\cdot\bar{NE}}{|EF|\cdot|NE|}=\frac{4\cdot(-2)+2\cdot4}{\sqrt{20}\cdot\sqrt{20}}=\frac{-8+8}{20}=0\Rightarrow E=90^o
\cosF=\frac{\bar{EF}\cdot\bar{FM}}{|EF|\cdot|FM|}=\frac{4\cdot2+2\cdot(-4)}{\sqrt{20}\cdot\sqrt{20}}=\frac{8-8}{20}=0\Rightarrow F=90^o
\cosM=\frac{\bar{MN}\cdot\bar{FM}}{|MN|\cdot|FM|}=\frac{(-4)\cdot2+(-2)\cdot(-4)}{\sqrt{20}\cdot\sqrt{20}}=\frac{-8+8}{20}=0\Rightarrow M=90^o
\cosN=\frac{\bar{MN}\cdot\bar{NE}}{|MN|\cdot|NE|}=\frac{(-4)\cdot(-2)+(-2)\cdot4}{\sqrt{20}\cdot\sqrt{20}}=\frac{8-8}{20}=0\Rightarrow N=90^o
Все стороны равны, угол между сторонами прямой. Значит, EFMN - квадрат.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Денис121009 Денис121009  05.06.2019 12:00
Впрямоугольном параллелепипеде стороны основания равны 12 см и 5 см,а диагональ параллелепипеда наклонена к плоскости основания под углом 60 градусов.найдите объем параллелепипеда....
Celestialess32 Celestialess32  05.06.2019 12:00
Найдите площадь ромба,если его диагонали 38 и 4...
Ivan208280 Ivan208280  12.05.2020 12:03
Відрізок МК паралельний стороні DE трикутника DEP, DE=32cm, DP=40cm, MP=25cm. MK-?...
kkoluzhonokp08din kkoluzhonokp08din  12.05.2020 12:03
CG — биссектриса угла ECD,CE — биссектриса угла FCD.Вычисли углы DCG и FCD, если ∢ECD=69°.a) ∢DCG= °;б ДО 12.05.2020 В...
Элиза5511 Элиза5511  09.03.2021 06:46
Найди правильный расчет заштрихованной части фигуры...
annafycguvvv annafycguvvv  09.03.2021 06:47
Какой из рисунков будет параллельным, объясните ответ​...
7chappe 7chappe  09.03.2021 06:50
В треугольнике АВС известно, что АС=30,2дм, ∠В= 600,∠А= 900 . Найдите расстояние от точки А до прямой ВС....
butterflygirl1 butterflygirl1  09.03.2021 06:50
и еще лучшим ответом сделаю только По данным рисунка найдите радиус вписанной в равнобедренний треугольник окружности1Нужно использовать свойства трапеции 2находит основание...
87711077664ZE 87711077664ZE  09.03.2021 06:53
очень умоляю сделайте ВСЁ И СДЕЛАЮ ОТВЕТ ЛУЧШИМ И ПОТПИШУСЬ...
alenalapshna2 alenalapshna2  09.03.2021 06:53
Найдите радиус окружности, вписанной в равнобедренную трапецию, если боковая сторона трапеций 10 см, меньшее основание равно 4 см.​...

Популярные вопросы