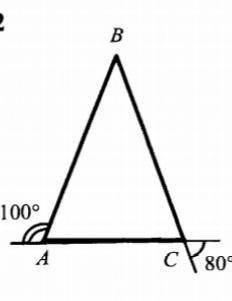
Докажите что abc равнобедренный

Для доказательства того, что треугольник ABC является равнобедренным, нам необходимо использовать определение равнобедренного треугольника.

Треугольник ABC считается равнобедренным, если он имеет две равные стороны или два равных угла. В данном случае нам дано, что сторонки AB и AC равны.

Пошаговое решение:
1. Обратите внимание на данное условие: AB = AC. Это означает, что сторона AB и сторона AC равны между собой.
2. Воспользуемся информацией, что если две стороны треугольника равны, то два угла, противоположные этим сторонам, также будут равны.
3. Посмотрите на угол BAC и угол BCA. Они являются противоположными сторонам AB и AC соответственно.
4. Так как стороны AB и AC равны, то соответствующие им углы BAC и BCA также равны между собой.
5. Итак, у нас есть два равных угла: угол BAC и угол BCA.
6. Следовательно, по определению, треугольник ABC является равнобедренным, так как имеет два равных угла BAC и BCA.

Таким образом, мы доказали, что треугольник ABC является равнобедренным с равными углами BAC и BCA.