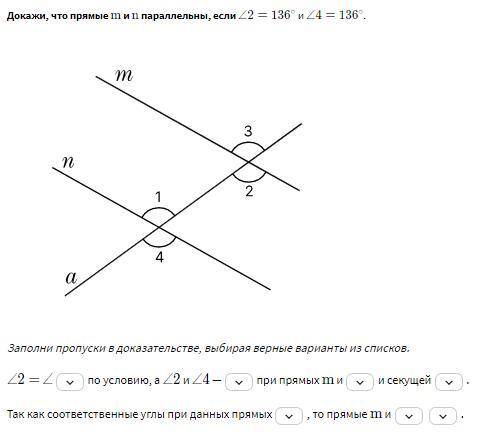
Докажи, что прямые m и n параллельны, если ∠2=136 и ∠4=136 Заполни пропуски в доказательстве, выбирая верные варианты из списков.
∠2= ∠ ? по условию, а ∠2 и ∠4 — ? при прямых m и ? секущей
Так как соответственные углы при данных прямых ?
, то прямые m и ? ?
Другие вопросы по теме Геометрия
Популярные вопросы
- Сочинение на тему какой подарок на день рождения я бы хотел получить...
2 - То, что крадётся по классу, как мышь. _о_с_ _ _ _ а...
3 - Выпишите сначала предложения с простым глагольным сказуемым в значении...
3 - Тип человека и общественное устройство энеолита...
1 - 1. маятник на поверхности земли колеблется с периодом 2с. чему будет...
3 - Можите составить все решения одной ? туристам надо было пройти 100...
3 - Решите уравнение 3(x-1)+4(x-1)=(x+2)...
2 - Є4 послідовні цілі числа. доведіть що добуток середніх чисел буде більшим...
1 - Как максимально ( для изложения ) предложение : кроме часов , минут...
3 - Вычислите произведение и запишите, как вы рассуждали. 5*5*6*4...
3
∠2= ∠ 4 по условию, а ∠2 и ∠4 — соответственные углы при прямых m и n секущей a
Так как соответственные углы при данных прямых равны, то прямые m и n параллельны
Углы, которые находятся по одну сторону от секущей и находятся на разных прямых, называются соответственными углами. В данном случае, ∠2 и ∠4 - это соответственные углы, так как они находятся на разных прямых m и n и находятся по одну сторону от секущей.
Теперь, чтобы доказать, что прямые m и n параллельны, нужно найти соответственные углы, которые равны между собой. В условии дано, что ∠2 = 136 и ∠4 = 136.
Таким образом, мы можем заполнить пропуски в доказательстве следующим образом:
∠2 = ∠4 по условию, а ∠2 и ∠4 — соответственные углы при прямых m и n секущей
Так как соответственные углы при данных прямых равны
, то прямые m и n параллельны
Доказательство заключается в том, что мы нашли соответственные углы ∠2 и ∠4, которые равны между собой. Согласно теореме, если углы соответственные и равны, то прямые, на которых они находятся, параллельны.
Итак, наши пропуски были заполнены, и мы доказали, что прямые m и n параллельны на основе равенства соответственных углов ∠2 и ∠4.