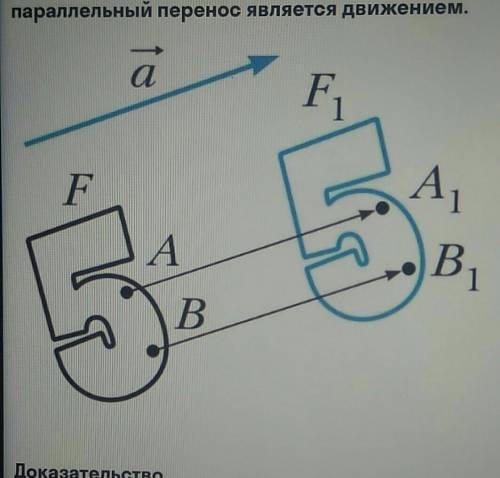
Доказательство. Пусть А(x1, y1 ) и B(x2; y2) — произвольные
точки фигуры F, точки А1 и B1 — Их
соответствующие образы при параллельном
переносе на вектор аст; п). Докажем, что
АВ
Имеем: AA1 = BB1 = . Векторы АА1 и BB
имеют координаты (L; ). Следовательно,
координатами точек А1 и B1 являются
соответственно пары чисел (L; ) и (
;).
Найдём расстояние между точками А и В:
AB =
Найдём расстояние между точками А и В1:
А1 В1
т. е.
Итак, мы показали, что AB
параллельный перенос сохраняет расстояние
между точками.​

mashka0414    3   06.04.2021 20:58    3