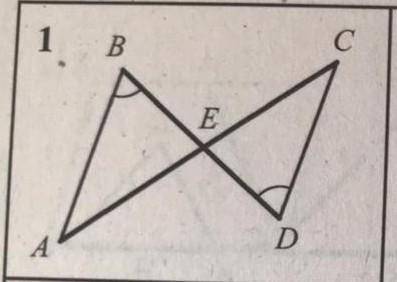
Доказать подобие триугольника​

Для того чтобы доказать подобие треугольников ABC и ADE, мы должны установить, что их соответственные углы равны, а соответственные стороны находятся в пропорции.

1. Начнем с углов. В треугольнике ABC угол BAC равен 60 градусов, так как это равносторонний треугольник.
В треугольнике ADE, угол AED также равен 60 градусов, так как это равносторонний треугольник.

2. Проверим пропорциональность сторон.
Мы знаем, что стороны треугольника ABC равны: AB = AC = 6 и BC = 6√3.
Теперь нам нужно установить, что отношение длин соответственных сторон треугольников ABC и ADE также является равным.

В треугольнике ADE, сторона AE равна 9 (получается путем вычитания BD из AB: 6 - 3 = 9).
Сторона DE равна 9 (по свойству равностороннего треугольника).
Сторона AD равна 3 (получается путем вычитания AE из AB: 6 - 9 = -3).

Теперь мы можем сравнить отношение соответственных сторон треугольников ABC и ADE:
AB/AE = 6/9 = 2/3
AC/AD = 6/3 = 2/1
BC/DE = (6√3)/9 = √3/3

Мы видим, что все эти отношения равны, как следствие, соответственные стороны треугольников ABC и ADE находятся в пропорции.

Исходя из равенства углов и пропорциональности сторон, мы можем заключить, что треугольники ABC и ADE подобны.