1. Геометрия
  2. Доказать ha=bc/2r при любом

Доказать ha=bc/2r при любом треугольнике. (рис. 4)

chelbaeva77 chelbaeva77    2   26.06.2019 17:47    3

Ответы
креореглеонл креореглеонл  21.07.2020 12:59

Пусть угол при вершине треугольника равен α

Площадь равна половине произведения длин двух сторон на синус угла между

S=\dfrac{1}{2}\cdot b\cdot c \sin\alpha

По теореме Синусов:  \dfrac{a}{\sin \alpha}=2R~~~\Rightarrow~~~\dfrac{abc}{2S}=2R

Также площадь треугольника равна произведению половины основания на высоту: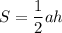 S=\dfrac{1}{2}ah, подставляем

\dfrac{abc}{2\cdot \frac{1}{2}ah}=2R~~~\Rightarrow~~~\dfrac{bc}{h}=2R~~~~\Rightarrow~~~~ \boxed{h=\dfrac{bc}{2R}}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
GMGasanovmm GMGasanovmm  24.02.2021 09:11
2.Используя теорему о внешнем угле треугольника, найдите угол В. В 16х+80 25х+100 1000 А С D...
azik55 azik55  24.02.2021 09:10
Sin7п/12cosп/12 - sinп/12cos7п/12...
Petrosyan31337 Petrosyan31337  24.02.2021 09:09
Куб стоит на плоскости (xy). Три ребра, исходящие из одной вершины, лежат на координатных осях, как показано на рисунке. Найдите координаты всех вершин куба, если ребро...
Hikena Hikena  13.07.2019 23:40
Стороны параллелограмма, заключающие угол 45°, равны 5 см и 8\sqrt{2} см. определите меньшую диагональ параллелограмма....
arinaantonuyk arinaantonuyk  09.07.2019 05:30
Дан прямоугольный треугольник с гипотенузой 5 и катетом 3. в1. найдите периметр данного треугольника. в2. найдите площадь данного треугольника. в3. найдите синус большего...
Соня12811 Соня12811  09.07.2019 05:20
Втреугольнике abc известно что угол bac 62 ad биссектриса найдите угол bad...
Дерижабль Дерижабль  10.09.2020 09:35
1.2. Изобразите: а) две пересекающиеся прямые;б) плоскость и непересекающую ее прямую;в) две пересекающиеся плоскости.​...
Znanija1821 Znanija1821  10.09.2020 09:25
Дан треугольникMNK.Луч с началом в точке М ,не слвпадашщий ни с какой из сторон треугольника,пересекает сторону треугольника в точке А.Между какими точками находится точка...
zlatoslava2p08lf0 zlatoslava2p08lf0  11.09.2020 09:54
Кто несет ответственность за мирное развитие человечества​...
мим221 мим221  12.03.2019 12:00
Постройте ромб cdek .укажите все пары векторов,начала и концы которых с вершинами ромба...

Популярные вопросы