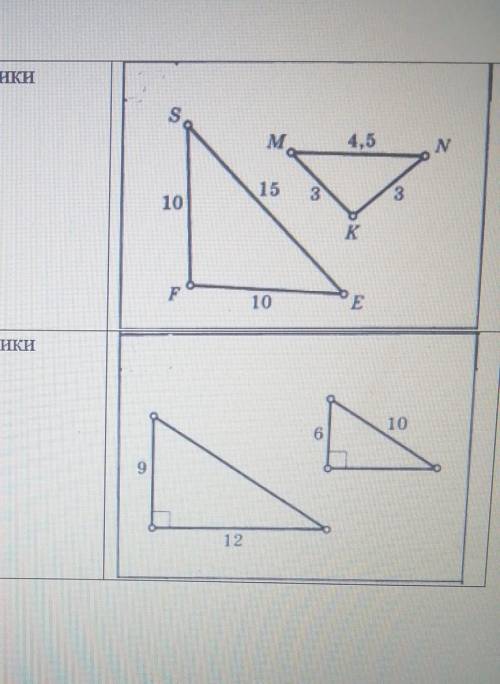
Доказать что треугольники SEF и MNK подобны
​

Для доказательства подобия треугольников SEF и MNK мы должны убедиться, что их соответствующие углы равны, а их соответствующие стороны пропорциональны.

1. Найдем соответствующие углы. Из данной фигуры мы видим, что угол SFE расположен против стороны SM, а угол NKM расположен против стороны NK. В треугольниках SEF и MNK эти углы обозначаются соответственно α и β.

2. Заметим, что углы EFS и KMN также являются соответствующими углами и равны друг другу. Обозначим их δ.

Итак, у нас получается следующее:
α = угол SFE = угол EFS
β = угол NKM = угол KMN
δ = угол EFS = угол KMN

3. Далее, чтобы убедиться в пропорциональности сторон треугольников, мы сравним их длины.

3.1. Сначала сравним соответствующие стороны SE и MN. Они обозначаются соответственно a и d.

Мы видим, что сторона SE разделена точкой F на две части, обозначим их длины как b и c.

Таким образом, мы имеем:
SE = SF + FE = b + c
MN = MK + KN = b + c

Из этого следует, что a = d = b + c.

3.2. Теперь сравним стороны EF и NK. Они обозначаются соответственно x и y.

Мы видим, что сторона EF разделена точкой S на две части, обозначим их длины как e и f.
Мы также видим, что сторона NK разделена точкой M на две части, обозначим их длины как g и h.

Итак, у нас получается:
EF = ES + SF = e + f
NK = NM + MK = g + h

Из этого следует, что x = y = e + f = g + h.

4. Теперь мы можем сделать вывод о подобии треугольников SEF и MNK.

Так как углы треугольников равны и их стороны пропорциональны, то треугольники SEF и MNK подобны по признаку подобия по углу-стороне.