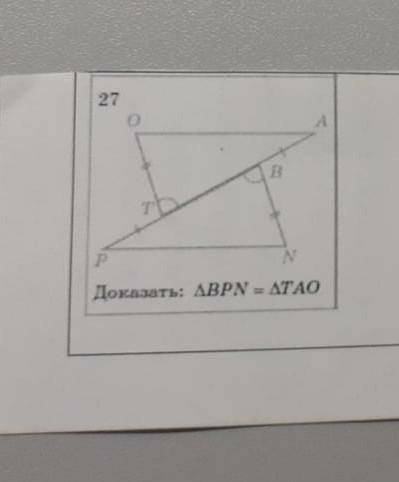
Доказать, что треугольник BPN=треугольнику TAO

TB - общая, PT = AB, значит AT = PB

угол T = угол B, AT = PB, OT = BN, значит треугольники равны по первому признаку (2м сторонам и углу между ними)

Объяснение:

Для доказательства равенства треугольников BPN и TAO, мы должны сравнить их стороны и углы.

1) Сравнение сторон:
- BN = OA: Это следует из условия, поскольку одна сторона прямоугольников является продолжением другой.
- BP = OT: Это следует из условия, поскольку одна сторона прямоугольников является продолжением другой.
- NP = AT: Это следует из условия, поскольку отрезок PN пересекает прямую PT, и высота PN делит отрезок PT на две равные стороны.

Таким образом, мы получаем, что длины всех сторон треугольника BPN равны длинам сторон треугольника TAO.

2) Сравнение углов:
- Угол BPN равен углу TAO: Это следует из условия, так как прямоугольники расположены параллельно и угол между прямыми BP и OT является прямым углом.

Так как треугольники BPN и TAO имеют равные стороны и равные углы, мы можем заключить, что они равны друг другу (соответствие треугольников или теорема SSS).

Таким образом, треугольник BPN равен треугольнику TAO.