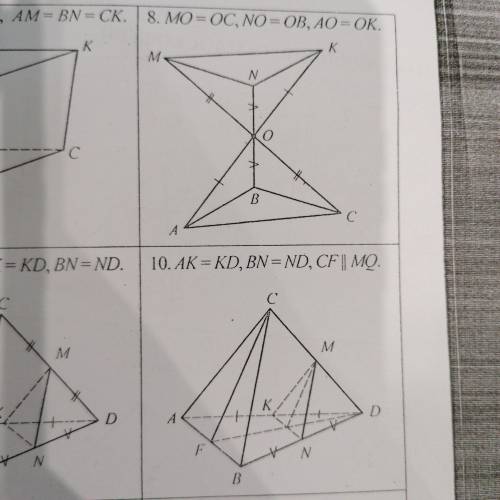
Доказать что плоскость ABC параллельна плоскости MNK, если MO=OC, NO=OB, AO=OK
И с 10
Другие вопросы по теме Геометрия
Популярные вопросы
- Сочинение какой я бы оставил след на земле...
1 - Твір-роздум ідея самопожертви напишіть не дуже великий 3_5 речень напишіть пошвидше...
2 - Abcd равнобедренная трапеция. ab=cd. ac перпендикулярна bd. bc+ad=18см. найти...
3 - Выберите правильный ответ неизменяемая часть речи-1)глагол 2)деепричастие 3)прилагаельное...
2 - Во сколько раз быстрее движится минутная стрелка в часах, чем часовая стрелка?...
3 - Идеи рисунков война глазами детей !...
1 - 1)алюминиевый брусок имеет массу 27 кг. чему равен его объём? (10 дм в кубе)...
1 - Масса соли, образовавшейся при нагревании оксида меди(2) массой 20 г. с серной...
2 - Исходя из реакции: mno(k)+c(гр)→mn(k)+со(г). вычислить стондартную энтольпию...
1 - По какому поводу было сказано: влияние,которое в старину сопутствовало владению...
1
Для начала, определим нормальные векторы для плоскостей ABC и MNK.
Для плоскости ABC возьмем два вектора, например AB и AC, и найдем их векторное произведение. По свойствам векторного произведения, вектор, полученный в результате, будет нормальным к плоскости ABC.
AB = B - A = (-3, 1, 2) - (1, 3, 2) = (-4, -2, 0)
AC = C - A = (5, -1, 2) - (1, 3, 2) = (4, -4, 0)
AB × AC = (-4, -2, 0) × (4, -4, 0) = (0, 0, 16)
Таким образом, нормальный вектор к плоскости ABC равен (0, 0, 16).
Проведем аналогичные вычисления для плоскости MNK.
MN = N - M = (5, -1, 2) - (3, -3, -2) = (2, 2, 4)
MK = K - M = (1, 3, 2) - (3, -3, -2) = (-2, 6, 4)
MN × MK = (2, 2, 4) × (-2, 6, 4) = (0, -16, 16)
Таким образом, нормальный вектор к плоскости MNK равен (0, -16, 16).
Теперь сравним нормальные векторы плоскостей ABC и MNK. Они имеют одинаковые координаты за исключением знака y-координаты. Это говорит о том, что они параллельны.
Таким образом, плоскость ABC параллельна плоскости MNK, при условии MO=OC, NO=OB, AO=OK, что и требовалось доказать.