Доказать,что диагонали куба пересекаются в одной точке и делятся точкой пересечения пополам.
Ответы
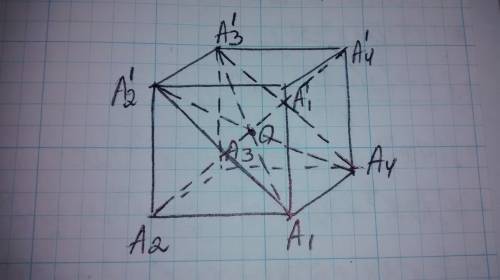
Рассмотрим какие-нибудь две диагонали куба, например А1А3' и А4А'2. Так как четырехугольники А1А2А3А4 и А2А'2А'3А3 — квадраты с общей стороной А2А3, то их стороны А1А4 и A'2A'3 параллельны друг другу, а значит, лежат в одной плоскости. Эта плоскость пересекает плоскости противолежащих граней куба по параллельным прямым А1А'2 и А 4А' 3. Следовательно, четырехугольник А4А 1A'2A'3 — параллелограмм. Диагонали куба А1А3' и А4А'2 являются диагоналями этого параллелограмма. Поэтому они пересекаются и точкой пересечения О делятся пополам.Аналогично доказывается, что диагонали А1А3' и А2А4' , а также диагонали А1А3' и А3А1' пересекаются и точкой пересечения делятся пополам. Отсюда заключаем, что все четыре диагонали куба пересекаются в одной точке и точкой пересечения делятся пополам. Доказано.
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия
Популярные вопросы
- Найдите стороны равнобедренного треугольника если его периметр равен...
2 - 15 слов на орфограмму гласные о и е после шипящих в суффиксах существительных...
1 - Можно ли лягушку отнести к хищным животным?...
3 - 2.раскройте скобки,употребляя глаголы в требующей форме,так чтобы получить...
1 - Причины присоединения западной украины и западной белоруссии к ?...
1 - 1.для чего школьники используют интернет? 2.как интернет в учебе? 3....
2 - H= 4м s = 30 см2 p(плотность)= 800 кг/м3( нефть ) f = ? не успеваю нужно...
3 - Как воспитывались крестьянские дети по однкнр...
3 - Запишите название частей слова корень - это...
3 - Со словосочетаниями: военный устав, воинский городок, враждебные взгляд,...
2