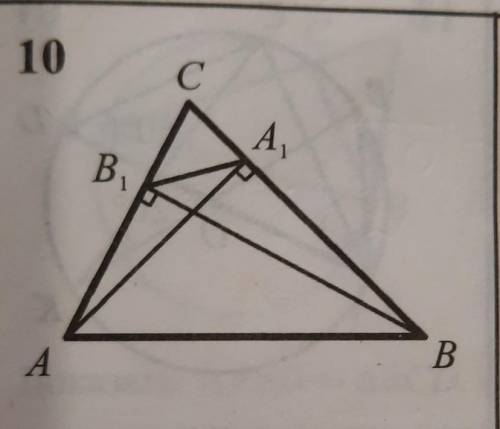
Доказать, что △АВС ~ △А1 В1 С1 и найти коэффициенты подобия.
Номер 10 и 12.
Другие вопросы по теме Геометрия
Популярные вопросы
- вас самостоятельная работа >...
1 - в основі прямої призми лежить ромб зі стороною 16 см і гострим кутом...
2 - Дослідити функцію f(x)=1/2x^4-4x^2 та побудувати її графік10 класс...
2 - Объясните химические и физические процессы происходящие в солнечной...
3 - Сторона ромба дорівнює 5 см одна діагоналей 6 см . знайдіть висоту...
2 - 2. Определить аргумент комплексного числа –1+i....
2 - Қазақ тілі: кеше, бүгін, ертең... Қазақ тілінің келешегі сізді толғандыра...
1 - Решите систему уравнений ...
2 - У нас сейчас самостоятельная, один из вопросов, нечего не понимаю...
3 - Решите пропорции 13/y = 26/15...
1
Условия подобия треугольников:
1) Углы треугольников должны быть равными.
В данном случае мы имеем прямые углы (углы, равные 90 градусам), угол В и угол В1, а также угол С и угол С1. Поэтому первое условие подобия треугольников выполнено.
2) Соотношение длин сторон треугольников должно быть одинаковым.
Для этого мы посчитаем отношение длин сторон треугольников и сравним их.
Стороны треугольника АВС:
AB = 6 см
ВС = 5 см
AC = 8 см
Стороны треугольника А1В1С1:
A1B1 = 12 см
В1С1 = 10 см
A1C1 = 16 см
Найдем отношение длин сторон, поделив каждую сторону треугольника АВС на соответствующие стороны треугольника А1В1С1:
AB/A1B1 = 6/12 = 1/2
ВС/В1С1 = 5/10 = 1/2
AC/A1C1 = 8/16 = 1/2
Мы видим, что отношение длин сторон в каждом случае равно 1/2. Поэтому второе условие подобия треугольников также выполнено.
Таким образом, мы доказали, что треугольники АВС и А1В1С1 подобны. Коэффициенты подобия равны 1/2.