Доказать, что △АВС ~ △А1 В1 С1 и найти коэффициенты подобия.

Чтобы доказать, что треугольники △АВС и △А1 В1 С1 подобны, нам необходимо убедиться, что их соответствующие стороны пропорциональны, а также углы равны.

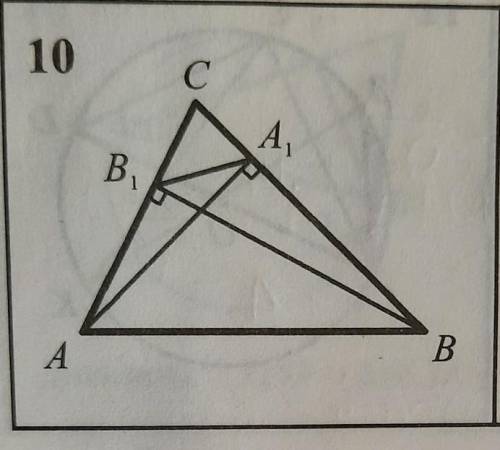
Давайте рассмотрим соответствующие стороны треугольников:

Сторона АВ в △АВС соответствует стороне А1В1 в △А1 В1 С1.
Сторона ВС в △АВС соответствует стороне В1С1 в △А1 В1 С1.
Сторона СА в △АВС соответствует стороне С1А1 в △А1 В1 С1.

Теперь нам нужно проверить, что эти стороны пропорциональны.

Для этого мы можем использовать теорему Безу. Она гласит, что если две тройки точек на одной прямой А, В, С и А1, В1, С1 пропорциональны, то и их парные отношения длин соответствующих сторон будут равны.

Итак, давайте найдем отношения длин соответствующих сторон:

AB / A1B1 = 7 / 3
BC / B1C1 = 10 / 15 = 2 / 3
CA / C1A1 = 8 / 4 = 2 / 1

Теперь найдем коэффициенты подобия треугольников △АВС и △А1 В1 С1:

Коэффициент подобия между сторонами АВ и А1В1 равен 7 / 3.
Коэффициент подобия между сторонами ВС и В1С1 равен 2 / 3.
Коэффициент подобия между сторонами СА и С1А1 равен 2 / 1.

Таким образом, мы доказали, что треугольники △АВС и △А1 В1 С1 подобны, и их коэффициенты подобия равны 7 / 3, 2 / 3 и 2 / 1.