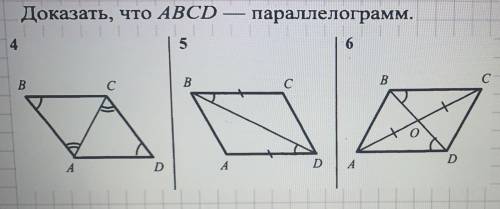
Доказать, что ABCD — параллелограмм
. (Только 6)
Другие вопросы по теме Геометрия
Популярные вопросы
- *как вы понимаете значение выражений травка заворсилась, листья...
1 - Составить предложение существительное.глагол.прилогательного...
1 - Выбирай и приписывай значение: сесть в лужу- зарубить на носу-...
2 - Хочется - морфемный разбор слова морфемный разбор - разбор слова...
3 - Как найти процент от числа и число от процента?...
2 - Решить в пятых классах школы 80 человек.из них отличники состовляют...
3 - Примеры влияния климата на быт население, характер построек, на...
2 - Стены и башни псковского кремля были сложены из местного известняка...
1 - Решите уравнение 1.4-3.5\0.15=2.3x-9\-1.5...
3 - Сочинение.вновь обратимся к репродукции картины алексея кондратьевича...
2
Объяснение:
1)
углы CBD и ADB равны
Один из признаков параллелограмма это паралельные противоположные стороны, углы CBD и ADB накрест лежащие углы , что доказывает параллельность сторон ВС и AD
2)
Четырёхугольник является параллелограммом, если его диагонали пересекаются и точкой пересечения делятся пополам.
диагональ BD делит диагональ АС пополам
что ещё раз доказывает что четырехугольник ABCD параллелограм
Объяснение:
Так как угол ∠СВО=∠АДВ как внутренние разносторонние, следовательно ВС || АД. Рассмотрим ∆ВОС и ∆АОД. Поскольку
ВС || АД, то ∠ВСО=∠ДАО, ∠ВОС=∠АОД как вертикальные, АО=СО – по условию, следовательно ∆ВОС=∆АОД по второму признаку, по стороне и прилежащим к ней углам. Тогда ВО=ДО и ВС=АД.
Рассмотрим ∆АОВ и ∆СОД, у них:
1) АО=СО
2) ВО=ДО
3) ∠АОВ=∠СОД, как вертикальные
Следовательно ∆АОВ=∆СОД, тогда АВ=СД.
Так как в четырёхугольнике АВСД АВ=СД, ВС=АД, ВО=ДО, АО=СО – противоположные стороны четырёхугольника АВСД равны, а также диагонали пересекаясь, делятся пополам, значит АВСД – параллелограмм
ДОКАЗАНО