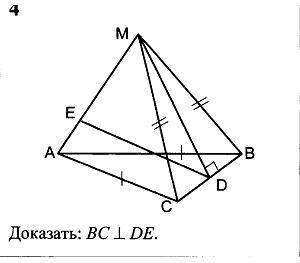
Доказать: BC перпендикулярно DE
Другие вопросы по теме Геометрия
Популярные вопросы
- 7. событие, которое произошло позже других: 1) грюнвальдская битва 2) присоединение...
2 - При нахождении значения выражения 34+3 марина ошиблась и выполнила умножене...
1 - Решите уравнение 5у+7у -0,024 =0,204 , x-0,64x=2,808 решите надо...
1 - Втабличном процессоре microsoft excel выделена группа ячеек d2: d7, сколько...
3 - Фразеологізм слово-сполучення розбити глека...
1 - Нужно выполнить морфологический разбор слова: расставлены....
1 - Прочитай .подчеркни буквы,написание которых не совпадает с произношением.?...
1 - Соляная кислота взаимодействует с выделение водорода а)zn б)cu в)ag...
2 - Площадь прямоугольника = 21 см квадратных. найти стороны если одна из них...
1 - Решите уравнение (x-1)(2x+6)=0; x²-16=0...
1
1. Дано: ABCD - квадрат, AC и BD - его диагонали, E - середина стороны AB.
2. Заметим, что треугольники CDE и CEB равнобедренные, так как CE = DE (как середина стороны AB) и углы CED и CDE равны 45 градусам (так как ABCD - квадрат).
3. Из свойства равнобедренных треугольников следует, что угол CBE равен углу CEB.
4. Также заметим, что угол CBE равен 45 градусам (так как ABCD - квадрат).
5. Из пунктов 3 и 4 следует, что углы CEB и CBE равны 45 градусам.
6. Таким образом, треугольник CBE является прямоугольным, так как у него есть угол, равный 90 градусам (45 градусов + 45 градусов).
7. Следовательно, отрезок BC перпендикулярен отрезку DE.
Таким образом, мы доказали, что отрезок BC перпендикулярен отрезку DE, используя свойства равнобедренных треугольников и квадрата ABCD.