До іть будь ласка 1)Знайдіть похідну функції y(x). що задана неявно рівнянням
2)Знайдіть похідну функції y(x). що параметрично
(тільки х зверу, а у знизу)
3)Знайти рівняння дотичної та номалі до графіка функції y= f(x) у точці абсцисою x_{0}
Другие вопросы по теме Геометрия
Популярные вопросы
- Максимально 2 . а) и б). хотя бы одно из них....
2 - Мо перпендикулярна до діагоналей паралело-грама abcd, які перетинаються...
2 - ответье на : 1)-запишите на месте пропуска название произведения...
2 - Назовите двух монахов, которые носили одинаковое имя, отчество...
1 - якими двома епітетами схарактеризовано пісню лолерей? чи можна...
3 - По какой цене m один из 8x^2-6x+9m^2=0 корней равен квадрату...
2 - Complete the text with the correct prepositions. b) ...
2 - 4. промінь падає на поверхню під кутом 30°. знайдіть кут заломлення,...
1 - She goes to school every satur day. составить предложения с положительным...
1 - Срисунка на с.78-79.определите,какие живые организмы обитаютна...
3
1.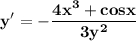
2.
3. ;
;
Объяснение:
1. Найти производную функции у(х), которая задана неявно уравнением:
Так как у является функцией от х, то будем рассматривать у³ как сложную функцию от х.
2. Найдите производную функции y (x), заданную параметрически.
Формула производной для функции, заданной параметрически:
Найдем x'(t) и y'(t):
3. Найти уравнение касательной и нормали к графику функции y= f(x) в точке абсциссой x₀.
Найдем производную:
Найдем значение функции и ее производной в точке x₀ = -3.
Уравнение касательной:
Получили уравнение касательной:
Уравнение нормали:
Получили уравнение нормали:
#SPJ1