Для острого угла a найдите sin a, если ctga = 4/5​

ответ:sina=5

Объяснение:

Объяснение:

Есть вот такое замечательное соотношение. В итоге получается: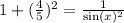

1+ 16/25= 1/ sin²(x)

41/25= 1/sin²(x)

25/41= sin²(x)

sin(x)= ±√25/41

ctg =4/5 , он положителен, а положителен он в 1 и 3 четвертях. По условию угол острый, то есть меньше 90 градусов, то есть подходит 1 четверть, т.к в 3 четверти угол будет лежать в промежутке (180°;270°) и считаться тупым. В 1 четверти синус положителен, то есть ответ sin(x)=√25/41