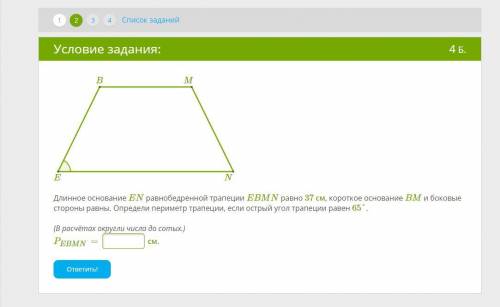
Длинное основание EN равнобедренной трапеции EBMN равно 37 см, короткое основание BM и боковые стороны равны. Определи периметр трапеции, если острый угол трапеции равен 65°. (В расчётах округли числа до сотых.)
Ответы
Для решения данной задачи, сначала нам потребуется использовать теорему косинусов для нахождения боковой стороны трапеции.
Пусть сторона BM и две боковые стороны имеют длину "х" см.
По теореме косинусов:
cos(65°) = (х^2 + х^2 - 37^2) / (2х * х)
cos(65°) = (2х^2 - 37^2) / (2х^2)
cos(65°) = (2х^2 - 1369) / (2х^2)
Теперь мы можем найти "х". Для этого решим получившееся уравнение:
(2х^2 - 1369) / (2х^2) = cos(65°)
2х^2 - 1369 = 2х^2 * cos(65°)
1369 = 2х^2 * (1-cos(65°))
1369 = 2х^2 * sin^2(32.5°)
х^2 = 1369 / (2 * sin^2(32.5°))
х^2 = 1369 / (2 * (0,524)^2)
х^2 ≈ 1369 / 0,5456
х^2 ≈ 2515,17
х ≈ √2515,17
х ≈ 50,15
Теперь, когда мы знаем значение "х", можем найти периметр трапеции.
Perimeter = EN + NM + MB + BE
Perimeter = 37 + x + x + x
Perimeter = 37 + 50,15 + 50,15 + 50,15
Perimeter ≈ 187,3 см
Ответ: Периметр трапеции примерно равен 187,3 см.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- Как нарисовать марко ройса поэтапно карандашом...
3 - Внароде этот святой считался покровителем лошадей...
3 - Составьте ребус к словам: узел, баррель...
2 - Which word is different? a) behind b) though c) across d) through...
1 - Какое течние у реки вятка: быстрое или медленное?...
3 - Кнеэлектролитам относится : серная кислота оксид калия гидроксид натрия сульфат...
1 - Скласти речення зі словом необачність....
1 - Изобразите векторы двух сил, которые по третьему закону ньютона равны друг другу...
2 - Тургенев. муму как относится гаврила к герасиму?...
3 - Как решить верное равенство за 1 класс3+5+1-2+3=?...
3