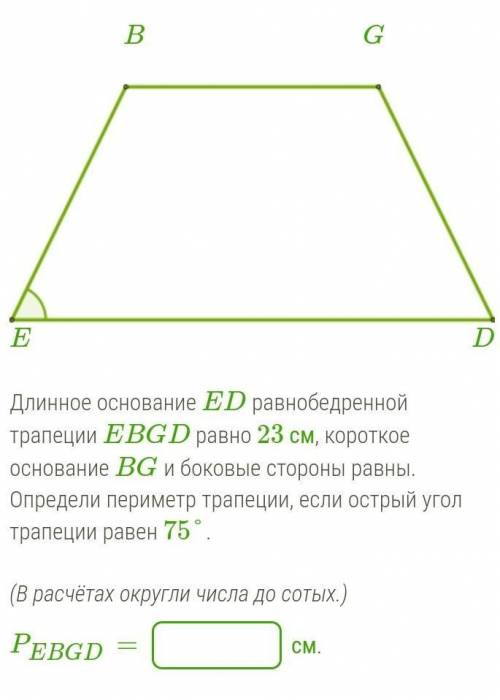
Длинное основание ED равнобедренной трапеции EBGD равно 23 см, короткое основание BG и боковые стороны равны. Определи периметр трапеции, если острый угол трапеции равен 75°.
(В расчётах округли числа до сотых.)
PEBGD= см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Ищу человека который может худеть за компанию Лет 12-15 Чтобы...
1 - Короче понятный пересказ бретской крепости с.с.Смирнова и побыстрее...
3 - Решите экспоненциальное уравнение: 5ˣ+10·5ˣ⁻²=7/25...
3 - Какая страна граничит с Австрией и Румынией? Дания, Венгрия,...
1 - Вопрос про оксиды и валентность 8 класс Задание: записать формулы...
3 - мне мне очень нужно . См. На фото. 2 упр, (б) можно не делать:)...
2 - Когда и где родился Владимир Путин?...
3 - Расшифруйте натальную карту. Буду очень благодарна!...
3 - Название какого метала несёт в себе волшебника?...
3 - Почему водный раствор триэтиламина становится пурпурным под действием...
1
Свойства равнобедренной трапеции:
1. Основания равны по длине. Значит, ED = BG.
2. Углы при основаниях равны. Значит, ∠B = ∠D.
Выходит, у нас есть два равных равнобедренных треугольника: BGD и EGD.
Следующий шаг - найти угол BGD.
Мы знаем, что сумма углов треугольника равна 180°.
Из этого можно найти угол BGD:
∠BGD + ∠D + ∠B = 180°
∠BGD + 75° + 75° = 180°
∠BGD + 150° = 180°
∠BGD = 180° - 150°
∠BGD = 30°
Теперь мы знаем, что угол G в треугольнике BGD равен 30°. Итак, с учетом этой информации, мы можем найти периметр трапеции.
Периметр трапеции - это сумма длин всех ее сторон. У нас есть две боковые стороны BG и GD, которые равны, и длинное основание ED.
Периметр трапеции:
P = BG + GD + ED
Так как BG и GD равны, мы можем записать:
P = 2(BG) + ED
Мы знаем, что BG = ED, поэтому:
P = 2(ED) + ED
P = 3(ED)
Осталось только найти длину основания ED.
Мы знаем, что сумма углов треугольника равна 180°.
Таким образом, у нас есть следующее уравнение:
∠EDG + ∠D + ∠EGD = 180°
∠EDG + 75° + 75° = 180°
∠EDG + 150° = 180°
∠EDG = 180° - 150°
∠EDG = 30°
Из этого следует, что угол EDG в треугольнике EGD равен 30°.
Мы также знаем, что сумма углов треугольника равна 180°.
Теперь мы можем найти угол GED:
∠GED = 180° - 75° - 30°
∠GED = 180° - 105°
∠GED = 75°
Так как у нас равнобедренная трапеция, ∠GED = ∠GDE = 75°.
Из угла 75° в треугольнике GDE следует, что угол EGD также равен 75°.
Теперь, используя угол EGD и длину основания ED, мы можем применить тригонометрию для нахождения значения BG:
sin(75°) = BG / ED
sin(75°) = BG / 23
Теперь мы можем решить это уравнение, чтобы найти значение BG.
BG = sin(75°) * 23
С помощью калькулятора, находим:
BG ≈ 23 * 0,966 = 22.3 (округляем до сотых)
Теперь мы можем найти периметр трапеции, используя найденные значения:
P = 2(BG) + ED
P = 2(22.3) + 23
P = 44.6 + 23
P ≈ 67.6 (округляем до сотых)
Итак, периметр трапеции PEBGD равен приблизительно 67.6 см.