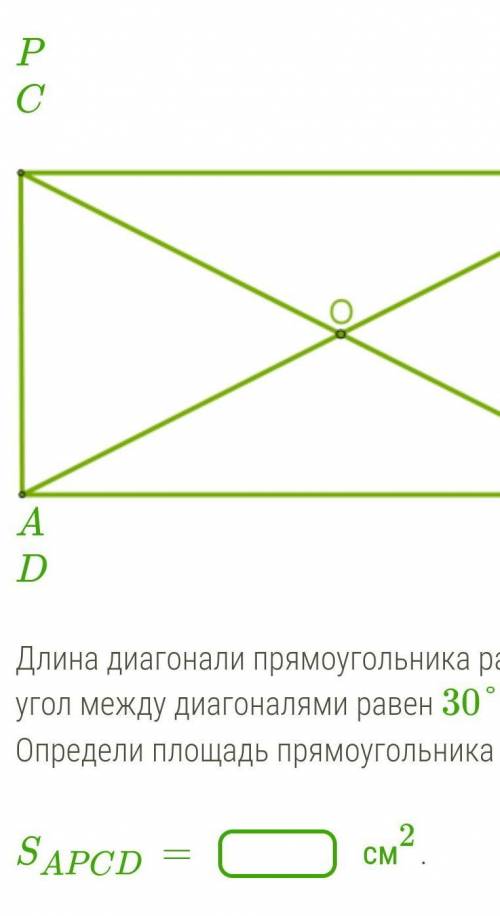
Длина диагонали прямоугольника равна 50 см, угол между диагоналями равен 30°. Определи площадь прямоугольника APCD.

SAPCD=
см2.
​

Для решения этой задачи, нам нужно использовать знания о свойствах прямоугольника и тригонометрии.

1. Сначала, обратим внимание на то, что мы знаем длину диагонали прямоугольника, которая равна 50 см.

2. Зная длину диагонали и угол между диагоналями, мы можем использовать тригонометрическую формулу для нахождения стороны прямоугольника.

3. Для этого, воспользуемся формулой косинуса:

cos(30°) = (AC^2 + AD^2 - 2 * AC * AD * cos(90°)) / AC * AD

4. Заметим, что в прямоугольнике длина диагонали равна гипотенузе прямоугольного треугольника, а длины сторон прямоугольника - это катеты этого треугольника.

5. В нашем случае, нам известна длина гипотенузы (50 см) и угол между катетами (30°). Пусть AC и AD - длины катетов.

6. Заметим также, что у нас есть прямой угол между катетами (угол CAD), поэтому cos(90°) равен 0.

7. Записав это в формуле, получим:

cos(30°) = (AC^2 + AD^2 - 2 * AC * AD * 0) / AC * AD

8. Упростив выражение, получим:

√3/2 = (AC^2 + AD^2) / (AC * AD)

9. Теперь, воспользуемся свойствами прямоугольника. Мы знаем, что противоположные стороны прямоугольника равны, значит:

AC = BD и AD = BC

10. Заменим AC на BD и AD на BC в полученном уравнении:

√3/2 = (BD^2 + BC^2) / (BD * BC)

11. Сократим BD на BD и BC на BC:

√3/2 = (BD + BC) / BC

12. Умножим обе части уравнения на BC:

√3/2 * BC = BD + BC

13. Упростим выражение:

√3/2 * BC = BD + BC
√3/2 * BC = 2BC

14. Поделим обе части уравнения на 2 и умножим на √3:

BC * √3/2 = BC

15. Получается:

√3/2 = 1

16. Это означает, что √3/2 = 1, что неверное утверждение. Следовательно, такое прямоугольника не существует.

Ответ: Невозможно определить площадь прямоугольника APCD, так как такого прямоугольника не существует.