Диаметр шара равен 20 .через его конец под углом 45°к нему проведена плоскость.найдите площадь полученного сечения.
Другие вопросы по теме Геометрия
Популярные вопросы
- Подчеркни грамматическую основу предложения. соседская лайка убежала на...
2 - Сочинение на тему: сравнительная характеристика героев повести ночь перед...
3 - Определите природные границы и главные особенности положения региона южный...
3 - Составить программу знакомство которая в конце диалога выдаёт резюме о...
3 - Установите последовательность иерархического соподчинения элементов нервной...
3 - Прочитайте тексты и установите соответствие между текстами и их заголовками:...
1 - Расстояние между двумя пристанями 150км. от этих пристаней навстречу друг...
3 - (m-n)(a+b-c) объясните , проходила но забыла ....
3 - Надо придумать 3-5 предложений. что бы ты сделал если бы оказался в вейне?...
2 - Гены в и с расположены в одной группе сцепления расстояние между ними...
1
Объяснение:
Пусть будет дан шар с центром в точке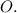
Через точку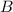 проведём плоскость под углов
проведём плоскость под углов 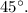
Пусть будет плоскость с центром в точке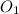 .
.
Тогда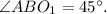
========================================================
Так как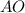 и
и 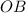 - радиусы данного шара
- радиусы данного шара 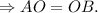
Радиус шара равен половине его диаметра.Т.е.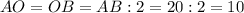 ед.
ед.
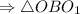 - прямоугольный.
- прямоугольный.
Сумма острых углов прямоугольного треугольника равнаТак как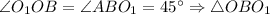 - равнобедренный.
- равнобедренный.
Пусть -
- 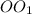 и
и 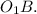
По теореме Пифагора: