1. Геометрия
  2. Диагонали разбивают выпуклый

Диагонали разбивают выпуклый четырёхугольник на четыре треугольника. Радиусы окружностей, описанных около этих треугольников, одинаковы и равны 10.
Найдите стороны четырёхугольника

tumoannasehko tumoannasehko    3   31.01.2022 00:29    8

Ответы
STEPNOJORSK STEPNOJORSK  31.01.2022 01:00

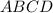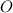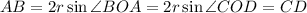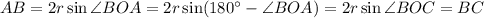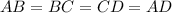Пусть рассматривается четырехугольник ABCD, а O -- точка пересечения диагоналей. Заметим, что во-первых, AB = 2r\sin\angle BOA = 2r\sin \angle COD = CD, а во-вторых, AB = 2r\sin\angle BOA = 2r\sin(180^{\circ}-\angle BOA) = 2r\sin \angle BOC = BC, следовательно, AB=BC=CD=AD.

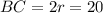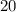Но тогда такой четырехугольник -- ромб. Поскольку \angle BOC = 90^{\circ}, то BC = 2r = 20, следовательно, все стороны четырехугольника равны 20.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Amirmusta Amirmusta  09.10.2019 18:23
Площадь прямоугольника со сторонами 9см и х равна s см2.выразите формулой зависимость s от х...
arina121212 arina121212  09.10.2019 18:24
Стороны треугольника равны 8 см, 10 см, 12 см. найдите середины сторон донного треугольника....
Jkbts Jkbts  09.10.2019 18:25
Ab-основание равнобедренного треугольника abc.докажите что окружность касающаяся сторон угла acb в точках a и b проходит через точку m-центр вписанной окружности в треугольник...
Lena121618 Lena121618  09.10.2019 18:27
Детская площадка имеет форму прямоугольника, площадь которого равна 66 м2. одна его сторона на 5 метр(-ов, -а) больше, чем другая. детской площадке необходимо построить бордюр....
potochnystanis potochnystanis  22.06.2019 11:40
Основание одной призмы-треугольник авс.угол с=90; ас=15; вс-20 см,высота призмы 12 см.найти площадь полной поверхности призмы....
мирали3 мирали3  22.06.2019 11:30
Расположите в порядке возврастания а-1; 1/а; а...
Karinago Karinago  22.06.2019 11:30
Найдите длину отрезка rs,учитывая, что: r(7; -3); s(10; 1);...
Inpeakfhdh Inpeakfhdh  11.03.2019 21:10
Биссектриса тупого угла параллелограмма делит его сторону на отрезки 6 и 10 см, считая от вершины гострого угла.вычислите площадь параллелограмма, если его острый угол равняется...
ivanovartem450p08ajg ivanovartem450p08ajg  11.03.2019 19:42
Зточки поза прямою проведено до неї дві похилі, одна з яких має довжину 10 см і утворює зі своєю проекцією на пряму кут 30°. знайдіть довжину другої похилої, якщо вона утворює...
anna4513 anna4513  11.03.2019 21:10
Периметр параллелограмма pqrt равен 24 см, а периметр треугольника pqt-18 см. найдите длину диагонали qt....

Популярные вопросы