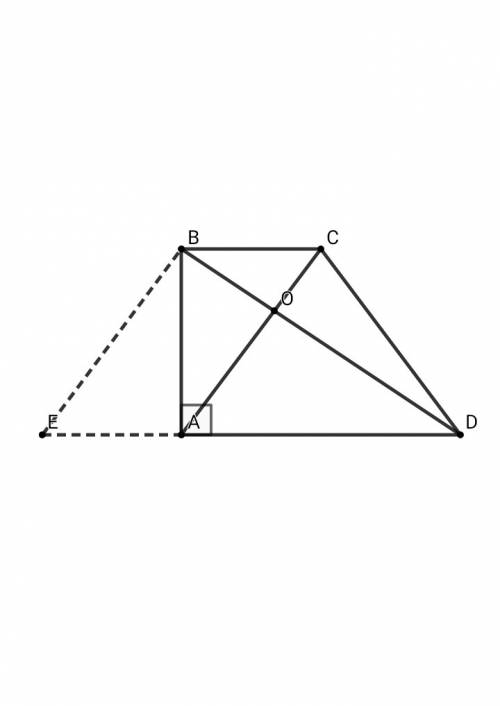
Диагонали прямоугольной трапеции abcd взаимно перпендикулярны. короткая боковая сторона ab равна 18 см, длинное основание ad равно 24 см. 1. короткое основание bc: bc= см. 2. длины отрезков, на которые делятся диагонали в точке пересечения o: короткая диагональ делится на отрезки co= см и ao= см. длинная диагональ делится на отрезки bo= см и do= см.ответить!
Ответы
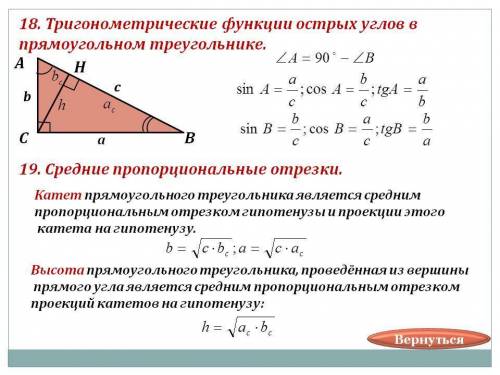
Из точки В проведём прямую ВЕ, параллельную диагонали АС, Е ∈ AD ⇒ BEAC - параллелограмм, ВС || ЕА, ВЕ || АСЗначит, ВС = ЕА , ВЕ = АС - по свойству параллелограммаАС⊥BD - по условию, ВЕ || АС ⇒ ВЕ⊥BD, AB⊥ED▪В ΔВЕD: пропорциональные отрезки в прямоугольном треугольнике ( см. приложение )АВ² = ЕА • АDEA = AB² / AD = 18² / 24 = 13,5 смВС = 13,5 см▪В ΔBAD: по теореме ПифагораBD² = AB² + AD² = 18² + 24² = 6²•( 3² + 4² ) = 36•25 = 30²BD = 30 смAD² = OD • BD ⇒ OD = AD² / BD = 24² / 30 = 576 / 30 = 19,2 смBO = BD - OD = 30 - 19,2 = 10,8 см▪В ΔBAD: AO² = BO • OD = 10,8 • 19,2 = 207,36 AO = 14,4 см▪В ΔАВС: ВО² = АО • ОС ⇒ ОС = ВО² / АО = 10,8² / 14,4 = 8,1ОТВЕТ: ВС = 13,5 см ; СО = 8,1 см ; АО = 14,4 см ; ВО = 10,8 см ; DO = 19,2 см.
ПОКАЗАТЬ ОТВЕТЫ


Другие вопросы по теме Геометрия
Популярные вопросы
- Решить уравнение m÷21=10 n÷17=9 k÷44=20...
2 - Как решить из двух городов расстояние между которыми 650 километров...
3 - Один из углов получающихся при пересечении двух прямых равен 87 градусов...
1 - Велосипед донгалагынын диаметрі 60 см. велосипед донгалагы 5 айналым...
1 - Мақал-мəтелдерде тақырыптары қандай? перевод на...
3 - Если мы хотим измерить температуру воды в сосуде необходимо...
2 - Дайте определение следующему понятию: государственная система...
3 - Махамбет отемисулы олендериндеги исатайдын образын жазу...
3 - Тектаническая структура заподной сибири...
1 - Время=50мин расстояние =600км .найти скорость...
3