Диагонали прямоугольника abcd пересекаются в точке о, угол адб = 30°,вд=10 см. найдите периметр треугольника аов.

см.

Объяснение:

По свойству прямоугольника,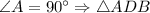 - прямоугольный.

см.

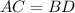По свойству диагоналей прямоугольника, и см.

Пусть - периметр треугольника AOB.

см.

P(AOB)= 15 см

Объяснение:

По свойству прямоугольника ABCD:

1) ∠A = 90°;

2) ∠DAC = ∠ADB;

3) ∠OAB = ∠OBA;

4) BO=OD.

Тогда  

Так как сумма внутренних углов треугольника AOB равна 180°, то  

∠AOB=180° – ∠OBA – ∠OAB = 180° – 60°– 60° = 60°.

Из ∠OBA = ∠OAB=∠AOB = 60° следует, что треугольник AOB равносторонний (см. рисунок). Отсюда

P(AOB)= 3•BO = 3•5 см = 15 см.