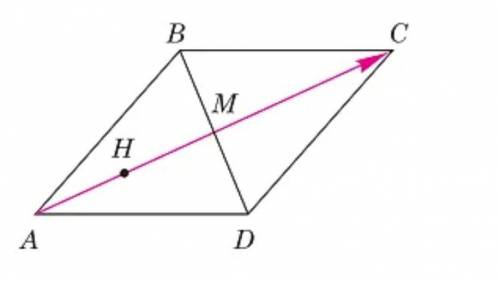
Диагонали парралелограмма АВСD пересекаются в точке М, точка Н-середина отрезка АМ. Найди если это возможно, такое число k, чтобы выполнялось равенство: а)АМ=k векторАС
б)векторМН=k векторАС
в)векторDM=k векторАС

Решение:
а)векторАМ↑↑ векторАС, поэтому искомое число k существует; |k|=векторАМ :__ и k __0(ноль). Т.к. диагонали парралелограмма точкой М делятся __(в отношении1:2, пополам), то |k|=___.

б) векторМН__вектор АС, поэтому исковое число k__(не существует, существует), |k|=векторМН:___ и k__0(ноль). По условию задачи точка Н-__(половина, середина) отрезка векторАМ, следовательно МН=½•__=½•(__АС)=__ АС, поэтому lkl=__.
Итак k=__.
в)векторыDM и ___ не коллинеарны, поэтому искомого значения k __ (не существует, существует).

на месте __ пропуски (заполните их), в скобках возможные варианты ответов.​

hchv    1   25.10.2020 09:55    34