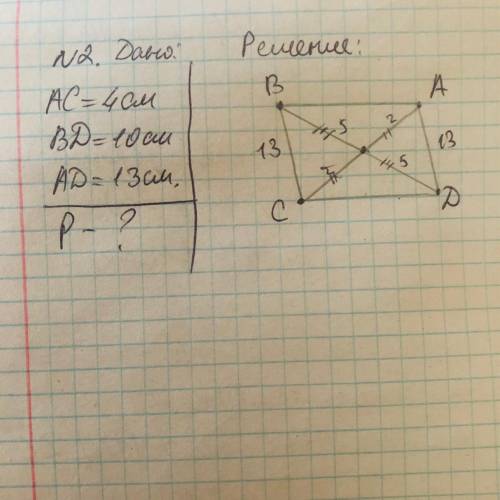
диагонали ac и bd параллелограмма abcd равны соответственно 4 см и 10 см, ad=13см. найдите периметр параллелограмма.
Другие вопросы по теме Геометрия
Популярные вопросы
- Cоставь и запиши план текста из трёх пунктов в ответе ты можешь использовать сочетания...
1 - [tex]xy = 12[/tex]мына теңдеудің қайсысы екі айнымалысы бар сызықтық теңдеу болады?...
3 - Все лирические отступления в романе евгений онегин пушкина...
3 - Придумайте свою новую технику изучения обществознания. например, приложение в телефоне...
2 - Проблемы рассказа карамзина,, сиерра морена !...
1 - Известно, что сумма длин всех рёбер куба равна 180 см, определи длину одного...
3 - Есть ли в слове рыбка проверочное слова есть ли в слове разбронили...
3 - Решите систему неравенств {х^2-10х+9≤0{10-3х 0...
3 - Как вы понимаете название в рассказе лёгкое дыхание ? ...
2 - Мороженное солержит 5 частей воды, 2 части молочного жира и 3 части сахара .сколько...
1
Обозначим стороны параллелограмма следующим образом:
AB = x (это равносильно CD = x)
AD = y (это равносильно BC = y)
По условию задачи нам известно, что диагонали AC и BD параллелограмма равны 4 см и 10 см соответственно, и AD = 13 см.
Мы можем использовать теорему Пифагора для нахождения значения сторон параллелограмма. В треугольнике ADB, применим теорему Пифагора:
AD^2 = AB^2 + BD^2
13^2 = x^2 + 10^2
169 = x^2 + 100
x^2 = 169 - 100
x^2 = 69
x = √69
Теперь мы можем найти значения сторон AB и CD параллелограмма:
AB = √69 см
CD = √69 см
Также известно, что AC это диагональ параллелограмма, и она равна 4 см. Рассмотрим треугольник ABC, где AC является гипотенузой:
AB^2 = AC^2 - BC^2
√69^2 = 4^2 - y^2
69 = 16 - y^2
y^2 = 16 - 69
y^2 = -53
Мы получили отрицательное значение y^2, что не является реальным значением, поэтому такой параллелограмм не может существовать. Возможно, в условии есть какая-то ошибка или опечатка.
В заключении, периметр параллелограмма ABCD не может быть найден, так как задача имеет неправдоподобные данные или ошибку.