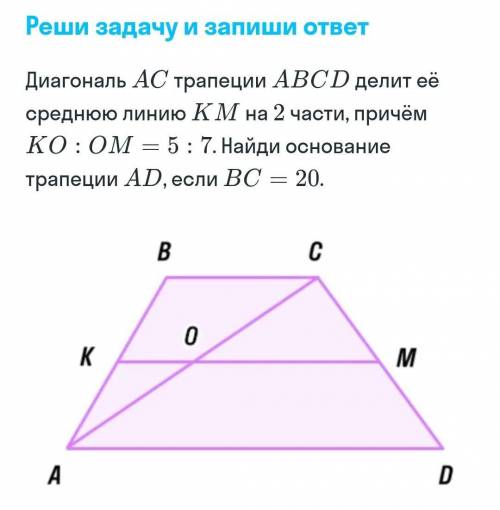
Диагональ АС трапеции ABCD делит её среднюю линию КМ на 2 части, причём КООМ — 5:7. Найди основание трапеции AD, если ВС = 20.​

Для решения данной задачи, нам понадобится использовать свойство диагоналей трапеции.

Сначала, воспользуемся информацией о соотношении КООМ. По данному условию, КО/ОМ = 5/7. Зная эту информацию, можно представить отношение КО/ОМ в виде КО = 5x и ОМ = 7x, где x - некоторое число.

Теперь обратим внимание на факт, что диагональ АС делит среднюю линию КМ на две части. Пусть точка пересечения диагонали АС и средней линии КМ называется N. Тогда, длина КН будет равна длине МН.

Определим длину КН:

КН = 5x + 7x = 12x.

Так как КН равна длине МН, то МН также равна 12x.

Теперь можем перейти к нахождению основания трапеции AD.

Сначала вспомним свойство средней линии трапеции: средняя линия равна полусумме оснований трапеции. В нашем случае, средняя линия равна 12x.

Теперь можем записать формулу для средней линии КМ: КМ = (ВС + АD)/2, где ВС равно 20 (по условию).

Подставляя известные значения, получаем: 12x = (20 + AD)/2.

Далее, умножим обе части уравнения на 2, чтобы избавиться от деления: 24x = 20 + AD.

Выразим основание трапеции AD: AD = 24x - 20.

Таким образом, основание трапеции AD равно 24x - 20.

В итоге, решив данное уравнение, получим значение основания трапеции AD.