Диагональ AC равнобедренной трапеции ABCD перпендикулярна стороне CD. Найдите AB, если AD = 4, AB^2+BC^2=11
Другие вопросы по теме Геометрия
Популярные вопросы
- Рассчитать значение падения напряжения по закону ома на участке медного...
2 - 1. закончите предложение: the emancipation proclamation freed: a) the...
1 - Вопрос: победил ли волк в словесном споре с ягнёнка? это из басни крылова...
1 - Вставьте пропущенные буквы; дайте толкование слов, используя конструкции...
1 - Разложите на множители выражение: 1) 4ab2 − 9а3; 2) x3 + 8y3; 3) с5 +...
3 - Какую цифру можно поставить вместо чтобы получить верное неравенство...
2 - Знайдіть сторони прямокутника трикутника периметер якого дорівнює 24...
2 - Составьте схему он отметил: у девушки красивое платье...
3 - Знайти 4 послідовні натуральні числа, якщо відомо, що добуток двох більших...
2 - Сравните положение и особенности природы крыма со странами средиземноморья....
2
√2 ..........................
Объяснение:
У равнобедренной трапеции диагонали равны, значит если AC ⊥ CD, то DB ⊥ AB. Проведём высоты BK и CF, AK = FD.
AD = 2AK + BC = 4 ⇒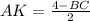 .
.
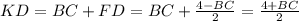
Высота, опущенная из вершины прямого угла на гипотенузу, есть среднее пропорциональное между проекциями катетовПо теореме Пифагора из прямоугольного треугольника ABK:
Из равенства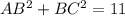 имеем
имеем 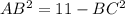
По теореме Виета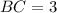 и
и  (лишний).
(лишний).
ответ: √2 .