Деревянный куб, ребро которого равно 12 см, распилили на две части: треугольную пирамиду и семигранник. (рисунок добавила)
найдите объем семигранника, если плоскость распила проходит через середины трех ребер куба, имеющих общую вершину.
Другие вопросы по теме Геометрия
Популярные вопросы
- Сочинение на тему « как я испугался » с планом 1 в лес за грибами...
1 - Надо написать причины конфликтов между родителями и детьми. в голову...
3 - Надо 20 . о чём вы задумались прочитав рассказ паустовского заичье...
2 - Сколько будет 1)4/5+3/4 2)5/6+3/8 3)9/10-5/6 4)3/4+3/14 5)7/10-1/4...
2 - Водній папці 10 аркушів кольорового паперу для уроків праці. для...
1 - Впервую столовую в одинаковых мешках завезли 300 кг крупы, а во...
1 - Решить цепочку ca(hco3)2 cacl2 agcl...
2 - Составить 8 предложений на украинском языке на тему початок весни...
2 - Округлите числа: а) до десятых: 6,041; 4,594; 0,123. б)до единиц:...
2 - Знаки которые указывают на необходимость бережного обращения к животным...
2
Vкуба = Vпир + Vсемигранн
Vсемигранн = Vкуба - Vпир
Vкуба =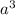 =12*12*12=1728(
=12*12*12=1728(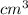 )
)
Если посмотреть на вершину куба(которая и вершина пирамиды) то все исходящие ребра будут взаимно перпендикулярны. Значит, два ребра образуют основание пирамиды, а третье - ее высота, все равны 1/2а.
Vпир = 1/3*Sосн * H = 1/3*(1/2*1/2a*1/2a)*1/2a=1/48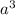 =36(
=36(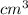 )
)
Vсемигранн=1692(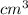 )
)