Даны вершины треугольника АВС А(4,1), В(24), С(0,1). Определите вид треугольника и найдите его периметр.
Другие вопросы по теме Геометрия
Популярные вопросы
- Найдите площадь параллелограмма ABCD, если АВ ответ или 30 или 15....
2 - Выполните упражнение Задание: определите, какими частями речи является выделенные...
1 - Визначення поняття онтогенез...
3 - Начертите в тетрадь и Дополните таблицу используя известные размеры прямоугольника...
1 - Какое отличие имеет геологическая история развития Северного Тянь-Шаня от остальных...
2 - Как протекает атмосферная коррозия железа, покрытого никелем, если покрытие нарушено?...
2 - Чи можна назвати Джульєтти слабодухою?...
3 - Найдите корни каждого уровнения 5y+12y2=0...
3 - Реши уравнение x*112-3054=9490, 54*x+960=3120 Решите уравнение...
2 - Объесните как вы понимаете название картины В.Н.Гаврилова последние васильки упр.448...
3
2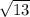 +4, равнобедренный треугольник
+4, равнобедренный треугольник
Объяснение:
Можно решать через вектора:
AB = (2-4, 4-1) = (-2,3) Длина AB = корень из ((-2)*(-2)+3*3) =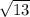
CB = (2-0, 1-4) = (2,-3) Длина CB = корень из (2*2+(-3)*(-3)) =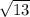
CA = (4-0,1-1) = (4,0) Длина AC =4
Итого: AB = CB, значит треугольник равнобедренный,
периметр = 2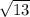 +4
+4
Можно просто через картинку, проведем точку К и найдем CB по теореме Пифагора: CB^2 = KB^2+CK^2 = 2^2+3^2 = 13
Отсюда CB =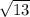
Аналогично AB
CA = 4 из рисунка
периметр = 2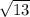 +4
+4