Даны векторы k(-1;2), s(5;-12), c(2;x). Найдите: a) cos k, s
b) число x, если k и c - коллинеарны
c) число x, если s и c - перпендикулярны

lluciferr01 3 25.10.2021 18:37 0

Question

Геометрия: Даны векторы k(-1;2), s(5;-12), c(2;x). Найдите: a) cos k, sb) число x, если k и c - коллинеарныc) число x, если s и c - перпендикулярны

lluciferr01 · Answer

Даны векторы k(-1;2), s(5;-12), c(2;x). Найдите: a)cos(∠k, s) ; b) число x, если k и c - коллинеарные; c) число x, если s и c - перпендикулярны.

Объяснение:

a)Косинус угла между векторами равен скалярному произведению этих векторов, деленному на произведение их длин.

Найдем длины векторов:

Длина вектора |k|=√( (-1)²+2²)=√(1 +4)=√5,

Длина вектора |s|=√( 5²+(-12)²)=√(25+144)=√169=13,

Скалярное произведение k*s=-1*5+2*(-12)=-5-24=-29

cos(∠k, s)= .

b) Два вектора коллинеарные ,если их координаты пропорциональны, значит для k(-1;2),c(2;x) :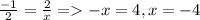 $\frac{-1}{2} =\frac{2}{x} = -x=4 , x=-4$ ;

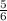c)Вектора перпендикулярны , если их скалярное произведение равно нулю : $\vec{s}*\vec{c}=5*2-12*x=0$ ⇒ 12x=10 , x= $\frac{5}{6}$ .

Даны векторы k(-1;2), s(5;-12), c(2;x). Найдите: a) cos k, sb) число x, если k и c - коллинеарныc) число x, если s и c - перпендикулярны